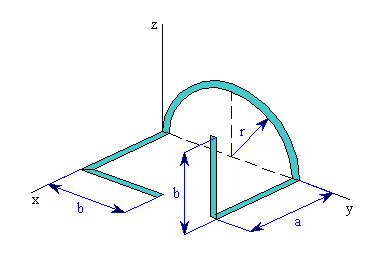
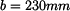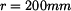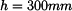Rovnováha hmotného bodu
Hmotný bod zavěšený na laně
Podepřený válec
Rovnováha tělesa
Moment síly
Výpočet momentu síly k bodu
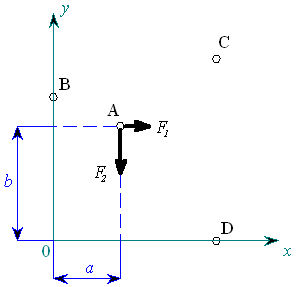
Dvě síly 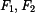 ležící v rovině mají působiště v bodě A viz obr.1.
ležící v rovině mají působiště v bodě A viz obr.1.
 |
 |
| obr. 1 |
Dáno:
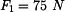
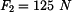
souřadnice bodu A:
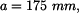
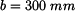
souřadnice bodu B:
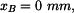
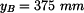
souřadnice bodu C:
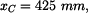
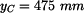
souřadnice bodu D:
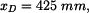
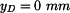 Určit:
Určit:
a) momenty síly
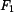
k bodům 0, B, C, D
b) momenty síly
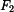
k bodům 0, B, C, D
Řešení:
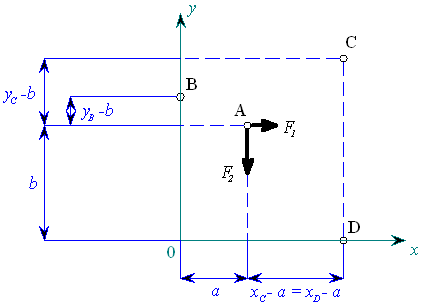 |
 |
| obr. 2 |
a) Nalezneme příslušná ramena síly
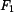
k bodům 0, B, C, D (obr. 2).
Moment síly
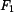
k bodu 0:
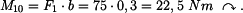 |
(1) |
Moment síly
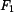
k bodu B:
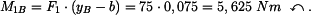 |
(2) |
Moment síly
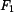
k bodu C:
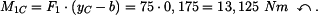 |
(3) |
Moment síly
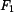
k bodu D:
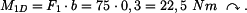 |
(4) |
b) Nalezneme příslušná ramena síly
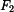
k bodům 0, B, C, D (obr. 2).
Moment síly
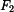
k bodu 0:
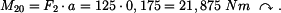 |
(5) |
Moment síly
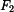
k bodu B:
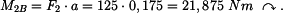 |
(6) |
Moment síly
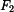
k bodu C:
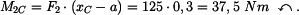 |
(7) |
Moment síly
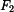
k bodu D:
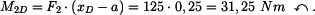 |
(8) |
TF-KS-02 Moment síly - Varignonova věta
TF-KS-03 Užití
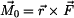
pro výpočet momentu
Užití vztahu  ve 2D.
ve 2D.
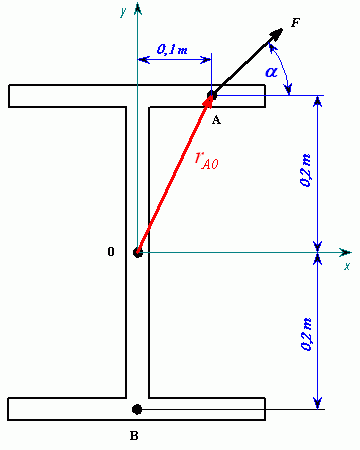
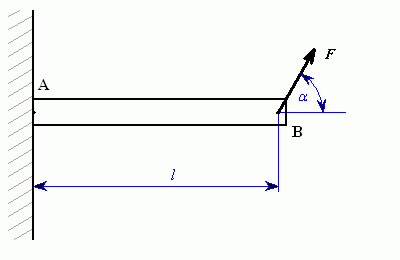
Síla
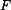
působí na těleso. Určete moment k bodu
0 a vzdálenost bodu
B od nosilky síly
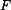
.
Obr.2
Dáno:
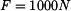
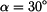
vzdálenosti viz obr.2
Určit: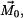
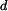
:
Řešení:
Sílu

a polohový vektor bodu A
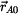
zapíšeme ve vektorovém tvaru
Pro určení vzdálenosti
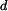
bodu B od nositelky síly
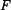
použijeme vektorový součin
kde
Pro rameno síly
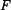
k bodu B platí
z toho
Zpracoval:
Zozulák Petr
TF-KS-04 - Silová dvojice
TF-KS-05 - Nahrazení síly silou a silovou dvojicí
Rovnováha tělesa
TF-KS-06 - Rovnováha tělesa v rovině 1
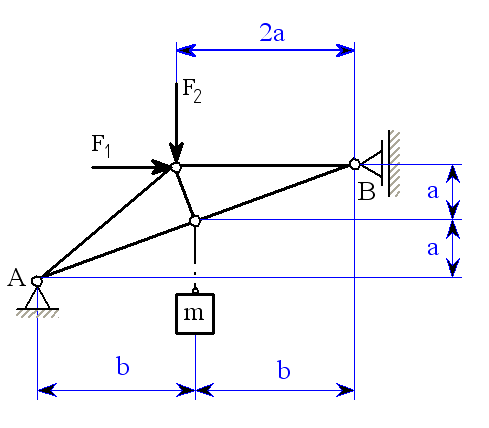 |
 |
| obr.1 |
Dáno:
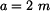
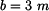

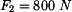
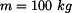
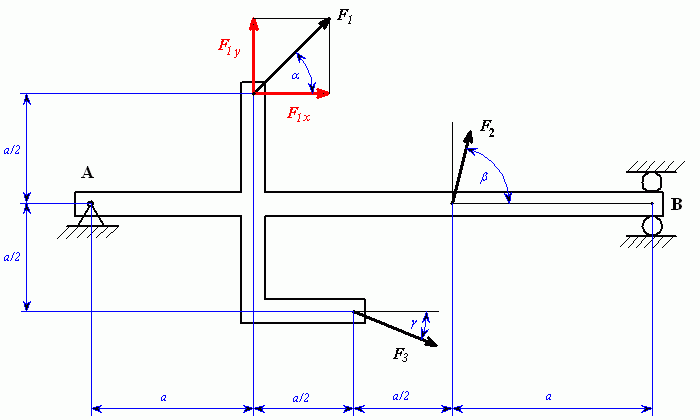
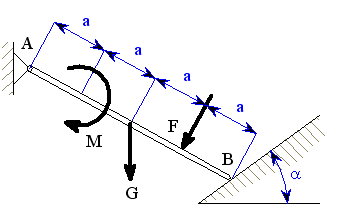
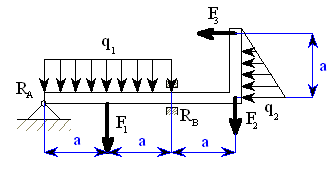
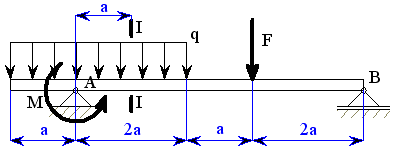
U daného tělesa tvořeného soustavou prutů určete reakce v uložení v bodech 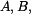 je-li zatíženo silami
je-li zatíženo silami 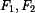 a břemenem o hmotnosti
a břemenem o hmotnosti 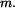
Určit:
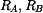
Řešení:
1. Uvolnění tělesa
 |
 |
| obr.2 |
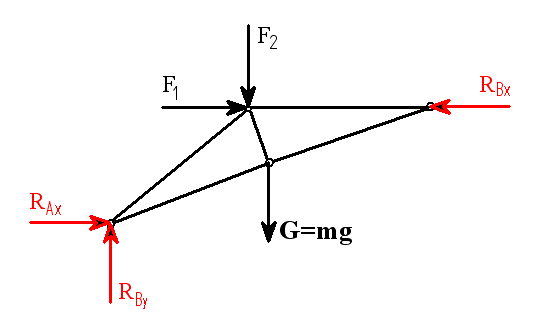
2. Rovnice rovnováhy
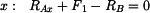 |
(1) |
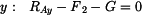 |
(2) |
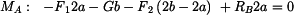 |
(3) |
3. Řešení soustavy tří rovnic o třech neznámých 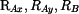
Z rovnice (3) určíme reakci 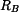
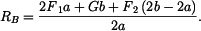 |
(4) |
Z rovnice (2) získáme
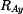
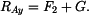 |
(5) |
Dosazením do rovnice (1) za 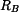 dostáváme
dostáváme
takže
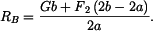 |
(6) |
4. Numerické řešení
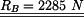
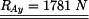
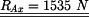
Zpracovala: Lucie Skálová
TF-KS-07 - Rovnováha tělesa v rovině 2
TF-KS-08 - Rovnováha tělesa v rovině 3
TF-KS-09 - Vnitřní silové účinky
Rovnováha soustavy těles v rovině
TF-KS-05 - Soustava těles v rovině
TF-KS-06 - Rovnováha soustavy těles 2
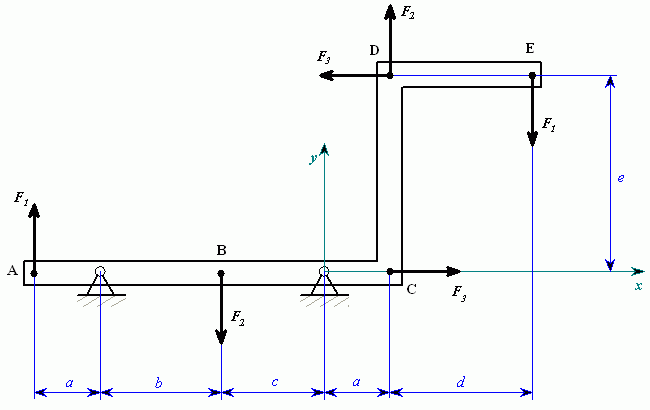
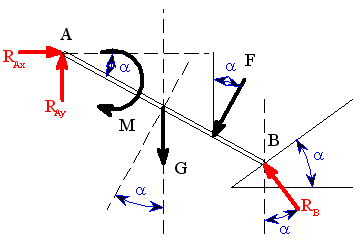
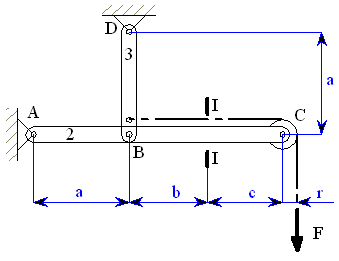
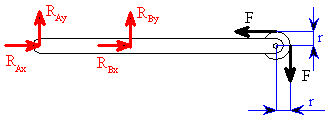
Rám (obr.1) je zatížen silami
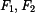
.
Dáno: 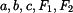
Určit: 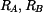
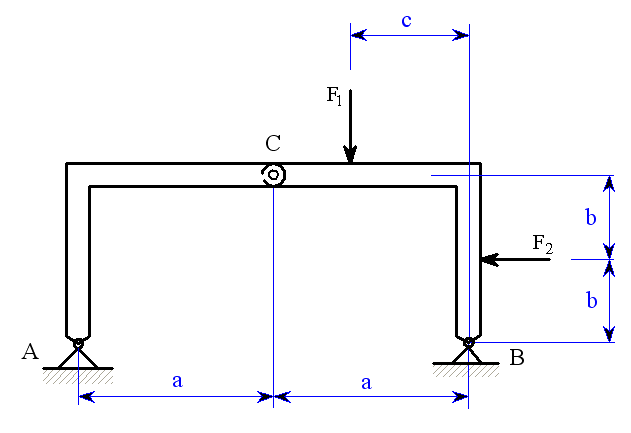
Řešení:
 |
 |
| obr.2 |
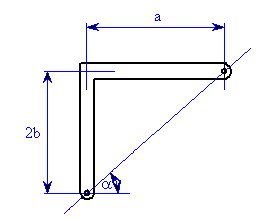
Protože těleso
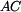
není zatíženo vnější silou a v kloubech

a
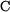
působí pouze reakce
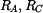
, jedná se o rovnováhu dvou sil a nositelka reakcí
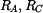
prochází body

a
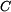
.
Směr nositelky je dán úhlem

.
1. Uvolnění
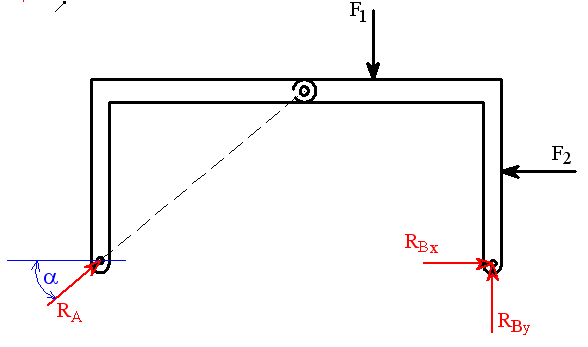 |
 |
| obr.3 |
2. Rovnice rovnováhy
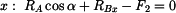 |
(1) |
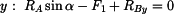 |
(2) |
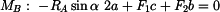 |
(3) |
Pozn.: x-ová složka  prochází bodem
prochází bodem 
 rameno je nulové a složka má nulový moment k bodu
rameno je nulové a složka má nulový moment k bodu 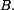
3. řešení soustavy rovnic (1), (2), (3)
Z rovnice (3) určíme 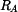
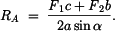 |
(4) |
Výraz (4) dosadíme do rovnice (1) a (2) a dopočítáme 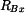 a
a 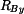
 |
(5) |
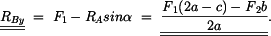 |
(6) |
Zpracovala: Lucie Skálová
Pasivní odpory
TF-KS-01 - Smykové tření 1
TF-KS-02 - Smykové tření 2
Těžiště
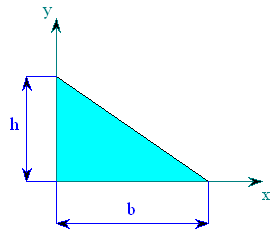
TF-KS-01- Trojúhelník
 |
 |
| obr. 1 |
Dáno:
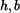 Určit:
Určit:
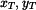
(integrací)
Řešení:
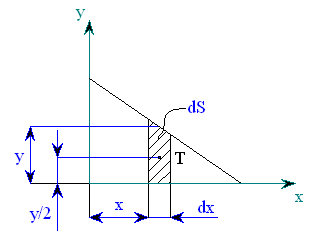 |
 |
| obr. 2 |
V trojúhelníku zvolíme elementární plochu dS (obr. 2).
kde souřadnici
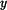
vypočteme z podobnosti
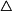
Výpočet souřadnice
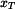
těžiště

je dán vztahem
Po dosazení za dS a úpravě
Výpočet souřadnice
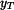
těžiště

provedeme analogicky
Po dosazení za dS a úpravě
Zpracoval: Radek Zbončák
Těžiště složených útvarů
Těžiště plošného útvaru
 |
 |
| obr. 1 |
Dáno:
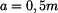 Určit:
Určit:
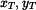
Řešení:
Vztahy pro výpočet souřadnic těžiště jsou
Po dosazení pro náš příklad dostaneme
Autor: Iva Petríková, Zpracoval: Radek Zbončák
Těžiště tenké čáry
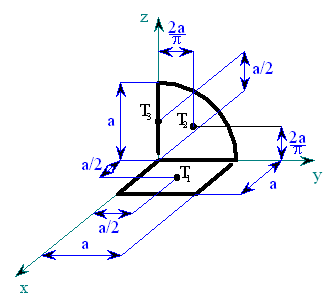 |
 |
| obr. 1 |
Dáno:
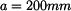 Určit:
Určit:
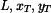
Řešení:
Útvar rozdělíme na tři dílčí útvary, jejichž těžiště známe.
Útvar č. 1 je tvořen obvodem čtverce v rovině xy a těžiště T
1 má souřadnice
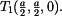
Útvar č. 2 je tvoří jedna čtvrtina kružnice a T
2 má souřadnice
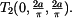
Útvar č. 3 je dán úsečkou a T
3 má souřadnice
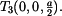
Obecné vzorce jsou
V našem případě
Výsledky:
Autor: Iva Petríková,
Zpracoval: Radek Zbončák
Těžiště prostorového útvaru
Těžiště plošného útvaru tvořeného třemi půlkruhy
Vypočítejte souřadnice těžiště plochy tvořené třemi půlkruhy podle obrázku.
Dáno:

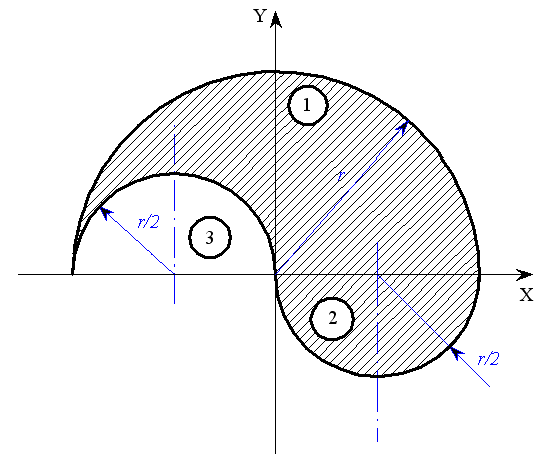 |
 |
| obr.1 |
Určit:
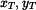
Řešení:
Podle II.věty Guldinovy-Pappovy platí pro půlkruhovou desku :
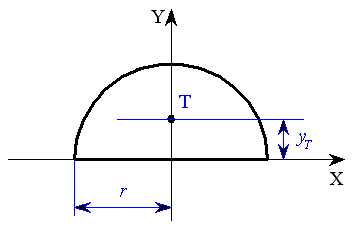 |
 |
| obr.2 |
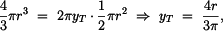 |
(1) |
Plochu rozdělíme na tři části, souřadnice jejich těžišť:
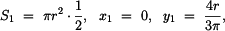 |
(2) |
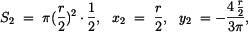 |
(3) |
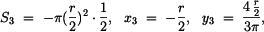 |
(4) |
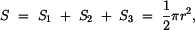 |
(5) |
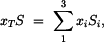 |
(6) |
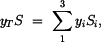 |
(7) |
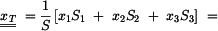 |
(8) |
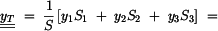 |
(9) |
Výsledek:
Autor: Iva Petríková,
Zpracovala: Lucie Skalova
Těžiště symetrického plošného útvaru
Určete souřadnice těžiště
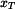
,
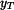
.
Dáno:
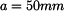
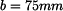
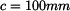

Řešení:
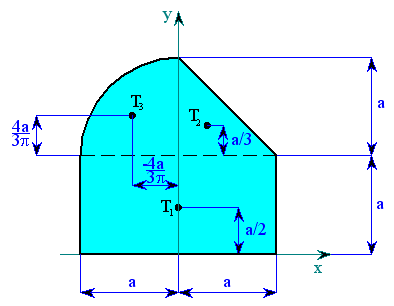
Plocha, u které máme určit těžiště, má osu souměrnosti rovnoběžnou s osou y ve vzdálenosti 2a. Z toho vyplývá, že
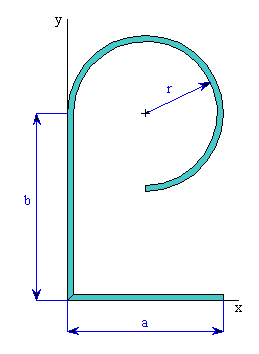
Zbývá určit souřadnici
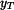
těžiště. Plochu rozdělíme na několik dílčích ploch, jejichž těžiště známe.
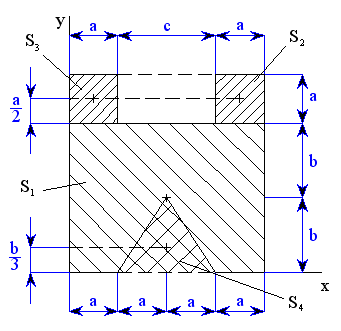
Souřadnice těžiště
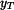
je dána vztahem
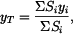
|
(1) |
kde 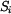 jsou jednotlivé plochy
jsou jednotlivé plochy 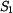 ,
, 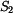 ,
, 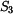 ,
, 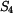 vyznačené na obrázku.
vyznačené na obrázku. 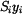 je statický moment plochy k ose x.
je statický moment plochy k ose x.
Celková plocha
Statický moment je
Statický moment útvaru, který v ploše chybí, odečítáme.
Po úpravě dostáváme
Dosazením do vztahu (1) dostáváme souřadnici
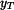
těžiště
Autor: Iva Petríková,
Zpracoval: Radek Zbončák
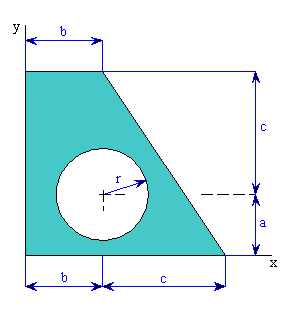
Těžiště plošného útvaru s kruhovým otvorem (neřešený příklad)
Těžiště plošného útvaru s půlkruhovým otvorem (neřešený příklad)
Těžiště složené tenké tyče 1 (neřešený příklad)
Těžiště složené tenké tyče 2 (neřešený příklad)
Těžiště prostorové složené tenké tyče (neřešený příklad)
Těžiště nehomogenního prostorového útvaru 1 (neřešený příklad)
Těžiště rotačního nehomogenního útvaru (neřešený příklad)
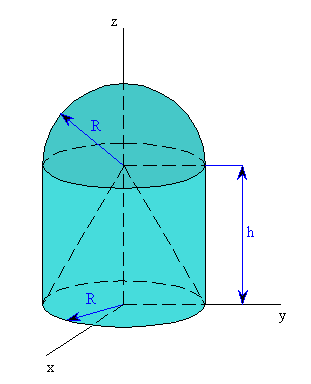
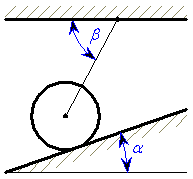
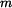 je zavěšen na dvou lanech 1, 2 podle obrázku 1.
je zavěšen na dvou lanech 1, 2 podle obrázku 1.
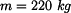
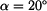
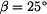

 (obr. 2).
(obr. 2).

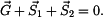
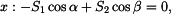
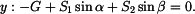
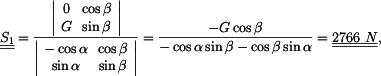
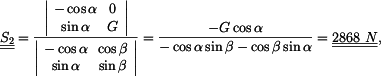
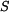 v laně a reakci
v laně a reakci  od podložky .
od podložky .
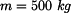
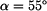
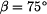
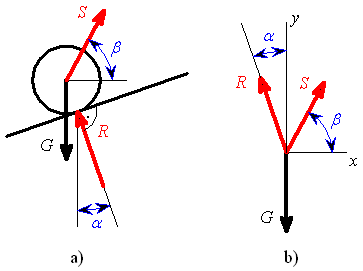
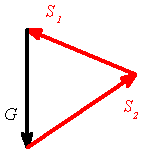
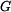 procházejí jedním bodem - středem válce (obr. 2b), jedná se o rovnováhu bodu. Zapíšeme vektorovou rovnici
procházejí jedním bodem - středem válce (obr. 2b), jedná se o rovnováhu bodu. Zapíšeme vektorovou rovnici
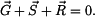
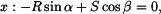

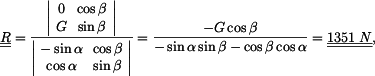
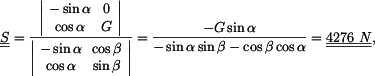
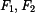 ležící v rovině mají působiště v bodě A viz obr.1.
ležící v rovině mají působiště v bodě A viz obr.1.

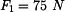
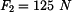
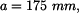
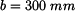
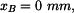
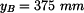
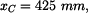
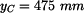
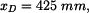
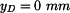
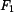 k bodům 0, B, C, D
k bodům 0, B, C, D 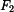 k bodům 0, B, C, D
k bodům 0, B, C, D 
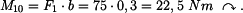
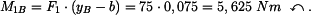
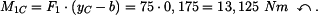
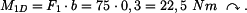
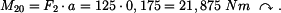
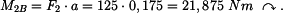
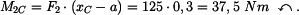
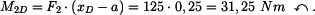
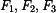 k bodu A.
k bodu A.
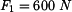
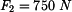
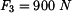
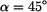
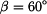
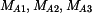
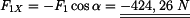
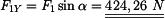

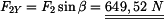
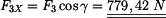
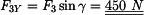

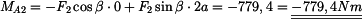
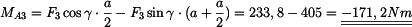
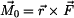 pro výpočet momentu
pro výpočet momentu ve 2D.
ve 2D.

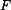 působí na těleso. Určete moment k bodu 0 a vzdálenost bodu B od nosilky síly
působí na těleso. Určete moment k bodu 0 a vzdálenost bodu B od nosilky síly 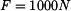
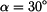
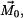
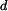 :
:
 a polohový vektor bodu A
a polohový vektor bodu A 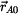 zapíšeme ve vektorovém tvaru
zapíšeme ve vektorovém tvaru
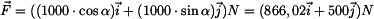
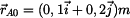
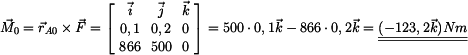
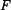 použijeme vektorový součin
použijeme vektorový součin
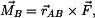
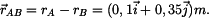
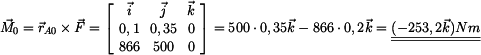
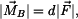
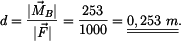
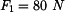
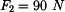
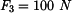
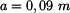
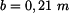
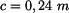
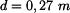
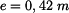
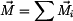 . Síly
. Síly 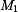 je dána vztahem
je dána vztahem
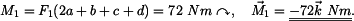
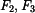
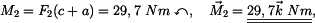
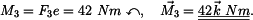
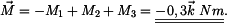
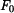 působící v bodě A a momentem.
působící v bodě A a momentem.
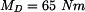
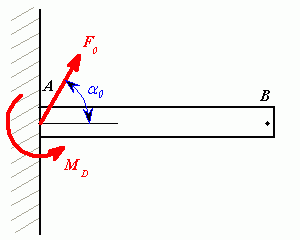
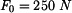
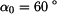

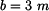

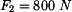
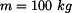
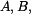 je-li zatíženo silami
je-li zatíženo silami 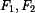 a břemenem o hmotnosti
a břemenem o hmotnosti 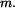
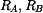

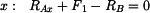
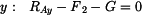
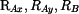
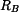
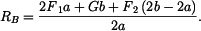
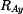
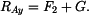
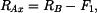
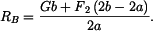
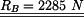
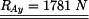
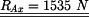
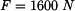
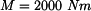
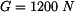
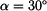
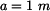
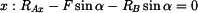
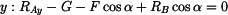
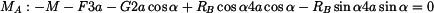
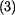 určíme reakci
určíme reakci 
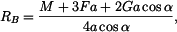
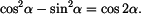
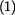 vyjde
vyjde
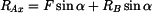
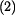
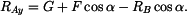
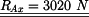
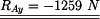
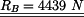
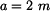
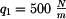
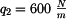
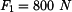
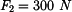
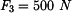
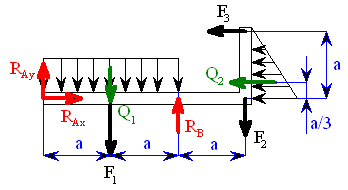
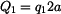 a
a 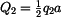 ležícími v těžišti (obr. 2).
ležícími v těžišti (obr. 2).
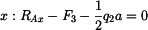
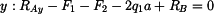
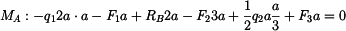
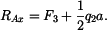


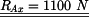
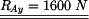

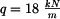
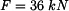
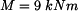
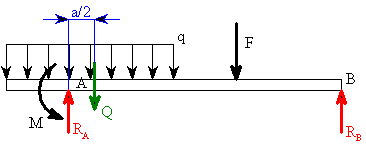
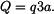
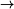
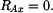
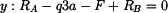
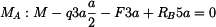
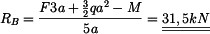
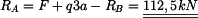
 a ohybového momentu
a ohybového momentu 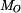 v řezu
v řezu  , normálová síla
, normálová síla 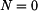
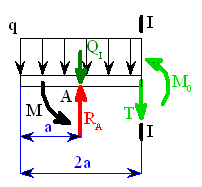
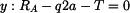
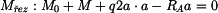
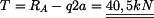
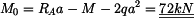
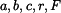
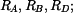
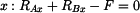
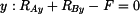
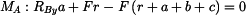
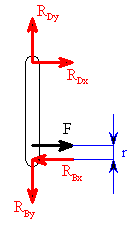
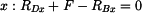
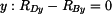
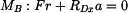
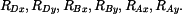
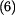 vyjádříme
vyjádříme
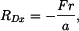
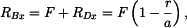
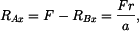
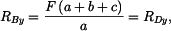
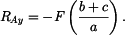
 normálovou silou
normálovou silou 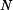 a ohybovým momentem
a ohybovým momentem 
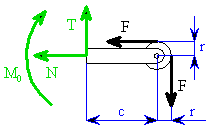
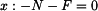
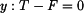
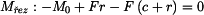
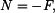
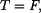
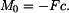
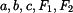
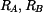


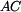 není zatíženo vnější silou a v kloubech
není zatíženo vnější silou a v kloubech  a
a 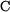 působí pouze reakce
působí pouze reakce 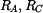 , jedná se o rovnováhu dvou sil a nositelka reakcí
, jedná se o rovnováhu dvou sil a nositelka reakcí 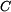 .
.
 .
.
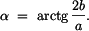

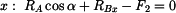
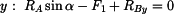
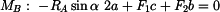
 prochází bodem
prochází bodem 
 rameno je nulové a složka má nulový moment k bodu
rameno je nulové a složka má nulový moment k bodu 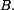
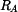
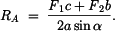
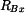 a
a 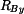

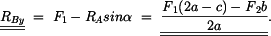
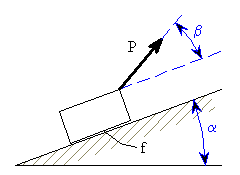
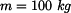
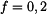
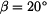
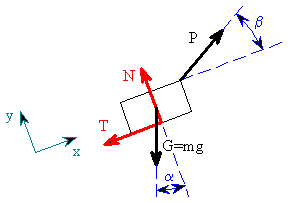
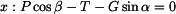
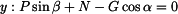
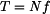
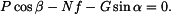
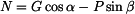
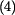
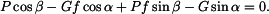
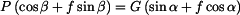
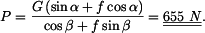
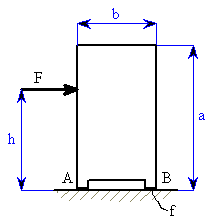
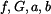
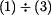 a připojíme vztahy pro třecí síly
a připojíme vztahy pro třecí síly 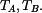
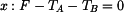
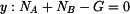

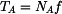
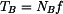
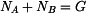
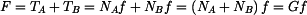
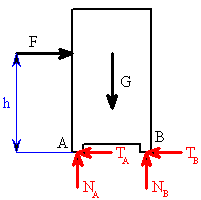
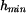 , kdy ještě nedojde k překlopení, určíme z momentové rovnice
, kdy ještě nedojde k překlopení, určíme z momentové rovnice 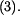
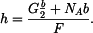
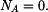
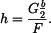

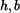
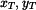 (integrací)
(integrací)

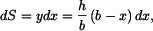
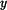 vypočteme z podobnosti
vypočteme z podobnosti 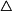
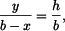
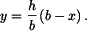
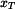 těžiště
těžiště 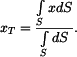
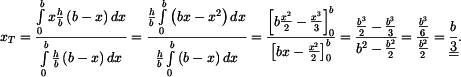
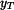 těžiště
těžiště 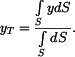
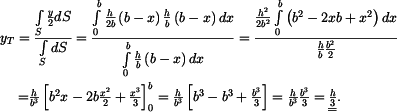

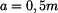
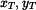
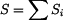
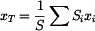
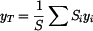
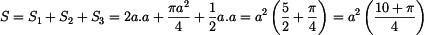
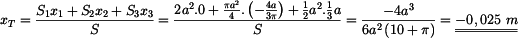
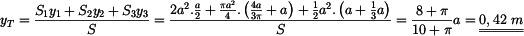

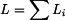
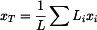
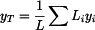
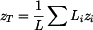
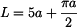
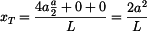
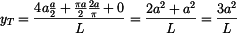
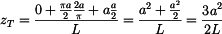
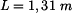
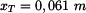
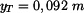
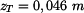
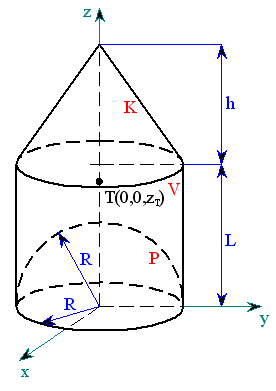


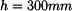
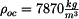
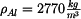
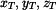 homogenního útvaru,
homogenního útvaru,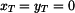
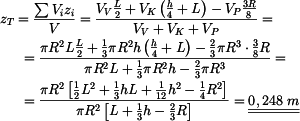
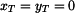
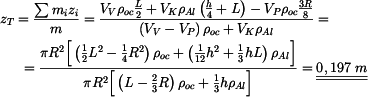



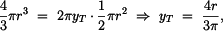
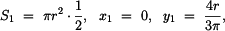
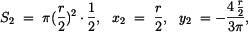
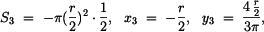
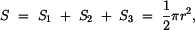
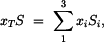
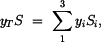
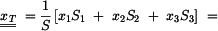
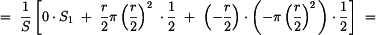
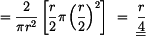
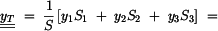
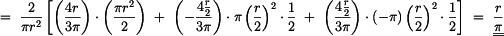
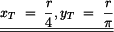
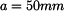
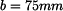
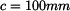

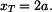

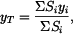
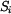 jsou jednotlivé plochy
jsou jednotlivé plochy 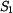 ,
, 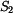 ,
, 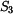 ,
, 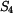 vyznačené na obrázku.
vyznačené na obrázku. 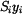 je statický moment plochy k ose x.
je statický moment plochy k ose x.
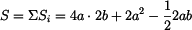
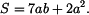
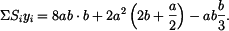
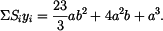

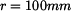
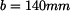
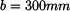
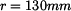
 štíhlé tyče zobrazené na následujícím obrázku.
štíhlé tyče zobrazené na následujícím obrázku.