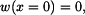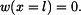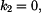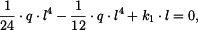Tah a tlak - příklady
Příklady z kapitoly "Tah a tlak"
Lano stálého napětí
Dáno :
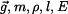
V homogenním tíhovém poli visí lano s proměnným průřezem , zatížené závažím o hmotnosti 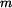 .
.
Určit :
Určete funkci , která vyjadřuje velikost průřezu lana tak, aby napětí v každém místě lana bylo rovno zadané hodnotě 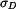 .
Určete prodloužení lana.
.
Určete prodloužení lana.
Řešení :
 |
 |
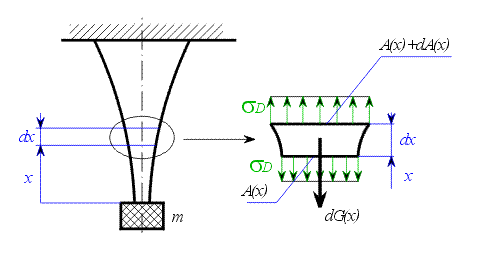
| Obr. 2 |
Zavedeme souřadný systém například s osou  o počátku na dolním konci lana a mířící nahoru.
o počátku na dolním konci lana a mířící nahoru.
Dvěma myšlenými řezy na souřadnicích  a
a 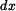 vymezíme infinetisimálně malý element lana.
vymezíme infinetisimálně malý element lana.
Na horní i dolní plochu elementu působí předepsané napětí 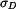 . Element má mimoto ještě vlastní tíhu
. Element má mimoto ještě vlastní tíhu 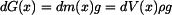 ,
kde
,
kde 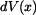 je jeho objem.
je jeho objem.
Rovnice rovnováhy pak má tvar
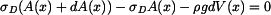 . . |
Podívejme se na objem 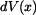 . Můžeme ho rozdělit na válec o objemu
. Můžeme ho rozdělit na válec o objemu 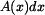 a na část , která tento válec obklopuje.
a na část , která tento válec obklopuje. 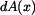 i
i 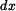 jsou
nekonečně malé veličiny. Objem druhé části bude tak nekonečně malou veličinou 2. řádu a můžeme ho zanedbat.
jsou
nekonečně malé veličiny. Objem druhé části bude tak nekonečně malou veličinou 2. řádu a můžeme ho zanedbat.
Rovnice rovnováhy potom vypadá takto :
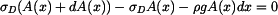 . . |
Po roznásobení dostaneme
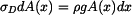 , , |
čili
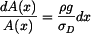 . . |
Integrujme obě strany rovnice
 , , |
čili
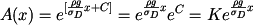 , , |
kde 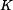 je integrační konstanta.
je integrační konstanta.
Hodnotu 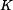 stanovíme z okrajové podmínky. Víme totiž , že i na dolním konci lana
stanovíme z okrajové podmínky. Víme totiž , že i na dolním konci lana 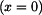 musí být napětí rovno
musí být napětí rovno 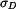 a vnitřní síla v tomto
místě je rovna pouze tíze závaží :
a vnitřní síla v tomto
místě je rovna pouze tíze závaží :
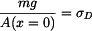 , , |
čili
a
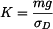 . . |
Výsledek:
Hledaná funkce je tedy
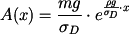 . . |
Napětí je v celé délce lana konstantní - 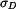 .
.
Poměrná deformace je
a prodloužení lana je
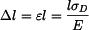 . . |
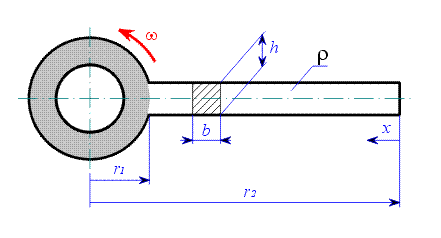
Rotující rameno
 |
 |
| Obr. 1 |
Určete :
dovolené otáčky
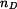
pomocí
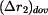
a
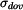
.
Řešení :
Zavedeme souřadnici  od konce ramene. Nejprve stanovíme velikost vnitřní síly v závislosti na
od konce ramene. Nejprve stanovíme velikost vnitřní síly v závislosti na  .
Vnitřní síla na souřadnici
.
Vnitřní síla na souřadnici  , je dána velikostí odstředivé síly, působící na vnější část ramene o délce
, je dána velikostí odstředivé síly, působící na vnější část ramene o délce  :
:
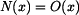 |
(1) |
Odstředivá síla 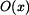 je rovna součinu hmotnosti
je rovna součinu hmotnosti  , poloměru na kterém rotuje těžiště ramene
, poloměru na kterém rotuje těžiště ramene 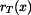 a druhé mocniny úhlové rychlosti
a druhé mocniny úhlové rychlosti
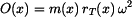 . . |
(2) |
Pro hmotnost platí
 , , |
(3) |
těžiště je uprostřed, tedy
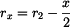 . . |
(4) |
Po dosazení (2) (3) a (4) do (1) dostaneme vnitřní sílu
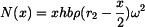 , , |
neboli po úpravě
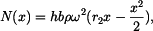
|
(5) |
Napětí  získáme jako podíl vnitřní síly a průřezu
získáme jako podíl vnitřní síly a průřezu
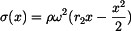
|
(6) |
a poměrnou deformaci pomocí Hookeova zákona
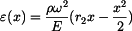 . .
|
(7) |
Všechny odvozené vztahy platí po celé délce ramene, tedy pro 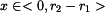 .
.
jednoduchým rozborem zjistíme, že napětí nabývá na uvedeném intervalu maxima pro 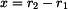 .
.
Musí proto platit
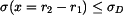 , ,
|
(8) |
čili
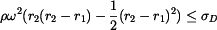 . .
|
(9) |
Po úpravě tak dostáváme
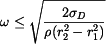 , ,
|
(10) |
neboli
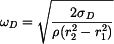 . .
|
(11) |
Dovolené otáčky jsou
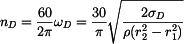 . .
|
(12) |
Po dosazení
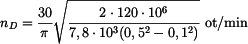
|
(13) |
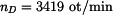 . . |
(14) |
Prodloužení ramene 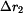 je rovno
je rovno
 , , |
(15) |
čili
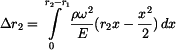 . . |
(16) |
Po integraci máme
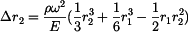 . .
|
(17) |
Podle zadání musí platit
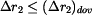 , , |
(18) |
tedy
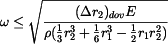
|
(19) |
a
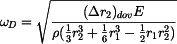 , , |
(20) |
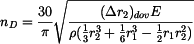 . .
|
(21) |
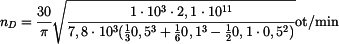
|
(22) |
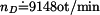 . . |
(23) |
Sloup v tíhovém poli I
 |
 |
| Obr. 1 |
Dáno :  .
.
Určete : průběh napětí ve sloupu a změnu jeho délky.
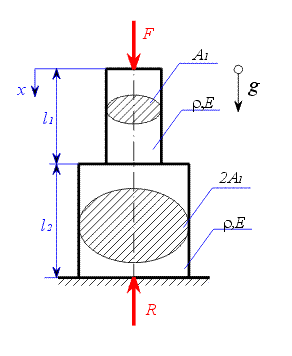
Sloup v tíhovém poli je znázorněn na obr. 1.
Řešení :
Zavedeme reakci v uložení (viz. obr. 1) a napíšeme rovnici rovnováhy
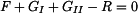 , , |
kde 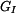 a
a 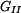 jsou tíhy horní a dolní části sloupu
jsou tíhy horní a dolní části sloupu
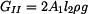 . . |
Stanovíme vnitřní sílu v horní části 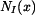 .
.
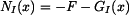 . . |
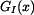 je tíha části sloupu nad řezem
je tíha části sloupu nad řezem
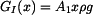 . . |
Vnitřní síla 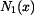 má tedy tvar
má tedy tvar
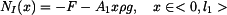 . . |
Vnitřní síla 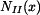 ve spodní části sloupu je dána silou
ve spodní části sloupu je dána silou 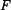 , tíhou celé horní části sloupu
, tíhou celé horní části sloupu 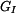 a tíhou
fragmentu dolní části
a tíhou
fragmentu dolní části 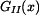 , který se nachází nad myšleným řezem.
, který se nachází nad myšleným řezem.
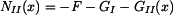 , , |
po dosazení
 . . |
Napětí v horní a dolní části 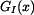 a
a 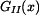 má tvar
má tvar
a
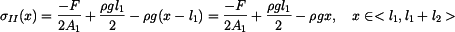 . . |
Poměrné deformace 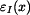 a
a 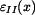 dostaneme z Hookeova zákona
dostaneme z Hookeova zákona
a
 . . |
Změnu délky 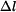 získáme integrací poměrné deformace
získáme integrací poměrné deformace
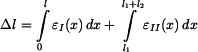 . . |
Po dosazení, integraci a úpravě dostaneme
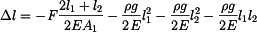 . . |
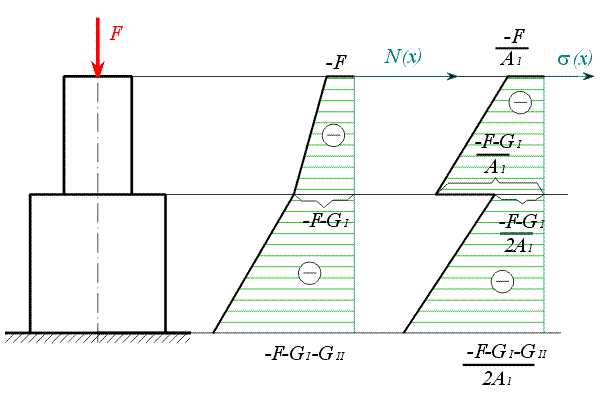
První člen představuje změnu délky sloupu způsobenou pouze silou 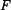 . Druhý člen je změna délky horní části sloupu od její vlastní tíhy,
třetí část je změna délky dolní části sloupu od její vlastní tíhy. Čtvrtý člen představuje změnu délky spodní části sloupu způsobenou tíhou horní části sloupu.
. Druhý člen je změna délky horní části sloupu od její vlastní tíhy,
třetí část je změna délky dolní části sloupu od její vlastní tíhy. Čtvrtý člen představuje změnu délky spodní části sloupu způsobenou tíhou horní části sloupu.
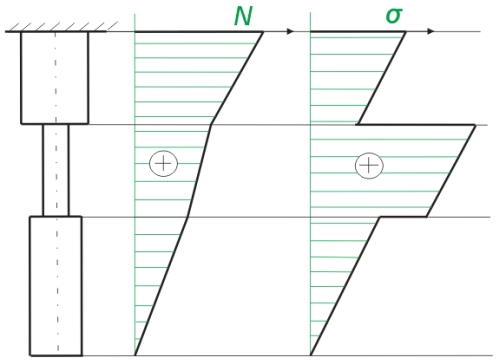
Průběh vnitřní síly a napětí je znázorněn na obr. 2.
Sloup v tíhovém poli II
 |
 |
| Obr. 1 |
Dáno :
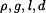
.
Určete : reakce a průběh napětí v tyči.
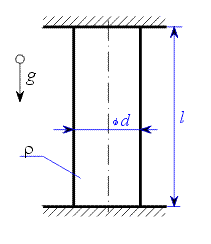
Tyč o délce 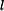 je upevněna podle obr. 1.
je upevněna podle obr. 1.
Řešení :
 |
 |
| Obr. 2 |
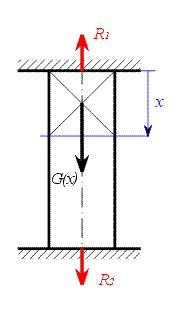
Zavedeme reakce a souřadnici  - viz. obr. 2. Jedná se o soustavu sil ležících v přímce, napíšeme proto jedinou rovnici rovnováhy.
- viz. obr. 2. Jedná se o soustavu sil ležících v přímce, napíšeme proto jedinou rovnici rovnováhy.
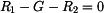 , ,
|
(1) |
kde tíha 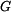 je tíha tyče
je tíha tyče
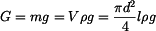 . .
|
(2) |
Úloha je jednou staticky neurčitá, musíme proto formulovat deformační rovnici. Vzhledem k uložení horního i dolního konce tyče platí
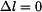 . .
|
(3) |
Hodnotu 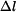 získáme integrací poměrné deformace
získáme integrací poměrné deformace
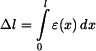 . .
|
(4) |
Po dosazení z Hookeova zákona máme
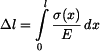
|
(5) |
a tedy
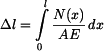 . .
|
(6) |
Vnitřní sílu 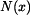 stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici
stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici  , (viz. obrázek 2) pak je vnitřní síla
, (viz. obrázek 2) pak je vnitřní síla 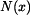 dána reakcí
dána reakcí  , která působí tahem a bude tedy mít kladné znaménko a tíhou
, která působí tahem a bude tedy mít kladné znaménko a tíhou 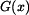 části nad řezem, která působí tlakem a bude tedy mít znaménko mínus.
části nad řezem, která působí tlakem a bude tedy mít znaménko mínus.
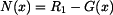 . .
|
(7) |
Pro 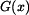 můžeme napsat
můžeme napsat
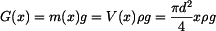 , ,
|
(8) |
tedy
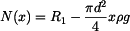 . .
|
(9) |
Z poslední rovnice dosadíme do vztahů (6) a (3) a po integraci dostaneme
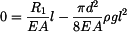 . .
|
(10) |
Vyjádříme 
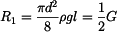 . .
|
(11) |
Z rovnice rovnováhy (1) dostaneme
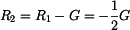 . .
|
(12) |
Určíme napětí z vnitřní síly (9), do níž dosadíme z (11).
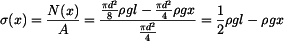 . .
|
(13) |
 |
 |
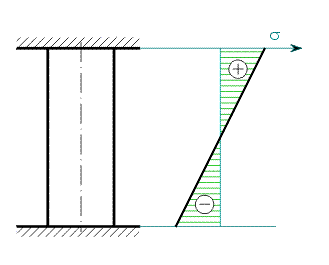
| Obr. 3 |
Na obr. 3 je znázorněna tyč a vedle graf průběhu napětí. Napětí se mění lineárně, v horní části tyče je tahové, v dolní je tlakové. Nulová hodnota
napětí je uprostřed tyče.
Sloup v tíhovém poli a změna teploty
 |
 |
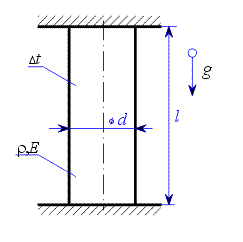
| Obr. 1 |
Dáno :
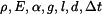
.
Určete : průběh napětí, reakce a poměrné deformace v tyči. Anylyzujte vliv velikosti a znaménka 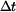 na výsledek.
na výsledek.
Tyč o délce 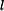 je upevněna podle obrázku 1 a poté se její teplota změní o
je upevněna podle obrázku 1 a poté se její teplota změní o 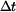 .
.
Řešení :
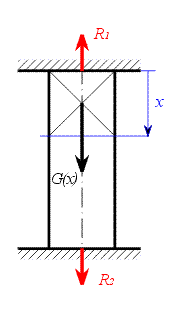 |
 |
| Obr. 2 |
Zavedeme reakce a souřadnici  - viz obr. 2. Pro soustavu sil ležících v přímce napíšeme
jedinou rovnici rovnováhy
- viz obr. 2. Pro soustavu sil ležících v přímce napíšeme
jedinou rovnici rovnováhy
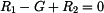 . .
|
(1) |
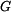 představuje tíhu celé tyče
představuje tíhu celé tyče
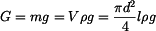 . .
|
(2) |
Úloha je jednou staticky neurčitá, musíme proto formulovat deformační rovnici. Vzhledem k uložení obou konců
tyče musí platit
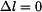 . .
|
(3) |
Hodnotu 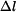 získáme integrací poměrné deformace
získáme integrací poměrné deformace
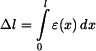 . .
|
(4) |
Tyč se deformuje nejen působením vnějších sil, ale také v důsledku změny teploty 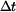 . Poměrná deformace
. Poměrná deformace  se skládá z komponenty způsobené silami
se skládá z komponenty způsobené silami 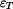 a z komponenty způsobené změnou teploty
a z komponenty způsobené změnou teploty 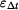 :
:
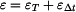 . .
|
(5) |
Pro 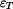 platí
platí
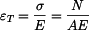 , ,
|
(6) |
kde 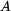 je průřez :
je průřez : 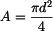 .
.
Pro 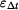 platí
platí
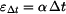 . .
|
(7) |
Vztah (4) vypadá po dosazení takto :
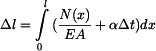 . .
|
(8) |
Vnitřní sílu 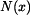 stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici
stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici  (viz. obr. 2), působí
tahem reakce
(viz. obr. 2), působí
tahem reakce  a tlakem tíha
a tlakem tíha 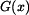 části nad řezem.
části nad řezem.
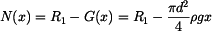 . .
|
(9) |
Z poslední rovnice dosadíme do (8) a (3) a po integraci dostáváme
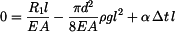 . .
|
(10) |
Vyjádříme reakci 
 . .
|
(11) |
Z rovnice rovnováhy (1) stanovíme 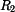 :
:
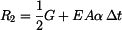 . .
|
(12) |
Z (11) dosadíme  do (9) a pro napětí pak platí
do (9) a pro napětí pak platí
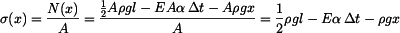 . .
|
(13) |
Analyzujme nyní velikost reakcí v závislosti na 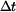 .
.
Pokud je 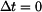 , pak
, pak 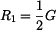 a
a 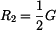 .
.
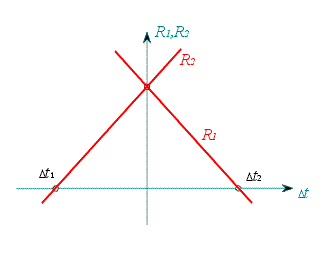 |
 |
| Obr. 3 |
Lineární závislost reakcí na 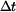 znázorňuje obr. 3.
znázorňuje obr. 3.
Je-li 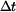 uvnitř intervalu
uvnitř intervalu 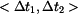 , pak obě reakce míří nahoru. Pro
, pak obě reakce míří nahoru. Pro 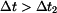 se mění znaménko u
se mění znaménko u  , která
pak míří dolů.
, která
pak míří dolů.
Naopak pro 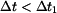 se obrací znaménko a tedy i směr reakce
se obrací znaménko a tedy i směr reakce 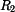 .
.
Stanovme nyní hodnoty 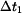 a
a 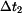 .
.
Pro 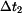 , platí že
, platí že 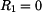 :
:
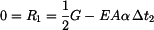 , ,
|
(14) |
čili
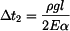 . .
|
(15) |
Pro 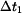 platí, že
platí, že 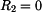 :
:
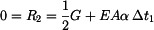
|
(16) |
a tedy
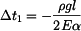 . .
|
(17) |
 |
 |
| Obr. 4 |
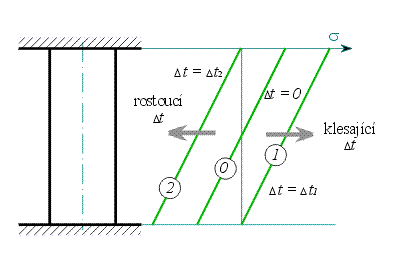
Podívejme se nyní na průběh napětí (vztah (13)). Pro 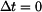 dostaneme závislost označenou v obr.4 číslem
dostaneme závislost označenou v obr.4 číslem 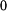 .
.
S rostoucím 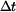 se průběh posouvá směrem doleva až při
se průběh posouvá směrem doleva až při 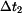 dosáhne nulové hodnoty na horním konci tyče - průběh
dosáhne nulové hodnoty na horním konci tyče - průběh 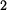 .
.
S klesajícím 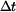 se průběh posouvá doprava a pro
se průběh posouvá doprava a pro 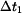 dosáhne nuly na dolním konci tyče - průběh
dosáhne nuly na dolním konci tyče - průběh 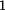 .
.
S dalším růstem, resp. poklesem teploty se průběhy posunují dál doleva resp. doprava.
Je-li 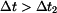 , pak je napětí v celé tyči záporné, tedy tlakové.
, pak je napětí v celé tyči záporné, tedy tlakové.
Je-li 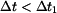 , je napětí v celé tyči kladné - tahové.
, je napětí v celé tyči kladné - tahové.
Je-li 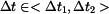 , je napětí v části tyče tahové a v části tlakové.
, je napětí v části tyče tahové a v části tlakové.
Trám na čtyřech prutech
Dáno :
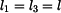
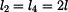
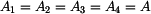
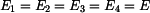
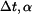

Určete :
Síly v prutech
Řešení:
Trám uvolníme, zakreslíme všechny síly, které na něj půsubí a zapíšeme rovnice rovnováhy.
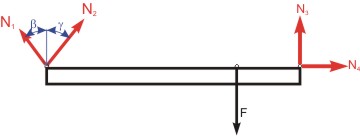 |
| Obr.1:Trám po uvolnění |
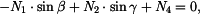 |
(1) |
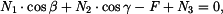 |
(2) |
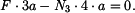 |
(3) |
Úloha je jednou staticky neurčitá
Zakreslíme trám v obecné poloze po deformaci a vyjádříme změny délek jednotlivých prutů. Trám je obecné těleso v rovině a jako takové má tři stupně volnosti. Jeho obecná poloha proto bude určena třemi parametry - vodorovným posuvem  , svislým posuvem
, svislým posuvem  a pootočením
a pootočením 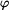 . Každý z těchto vlivů způsobí nějaké změny délek jednotlivých prutů. Skutečná změna délky každého prutu je pak dána jako změny délky od
. Každý z těchto vlivů způsobí nějaké změny délek jednotlivých prutů. Skutečná změna délky každého prutu je pak dána jako změny délky od  , od
, od  a od
a od 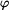 . Pro prut číslo
. Pro prut číslo 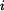 tedy můžeme psát:
tedy můžeme psát:
A. Změny délek od posuvu 
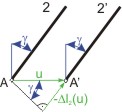 |
Obr.2:Změna délky prutu č.2,způsobená vodorovným posuvem 
|
Zvolíme si posuv  například vpravo. Na obr. 2 je znázorněn trojúhelník, vyjadřující změnu délky prutu č.2, způsobenou posuvem
například vpravo. Na obr. 2 je znázorněn trojúhelník, vyjadřující změnu délky prutu č.2, způsobenou posuvem  . Je zřejmé, že změna délky bude záporná, délka odvěsny trojúhelníka proto bude
. Je zřejmé, že změna délky bude záporná, délka odvěsny trojúhelníka proto bude 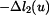 .
.
Platí:
a tedy
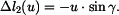 |
(4) |
Obdobně určíme
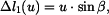 |
(5) |
Vodorovný posuv se projeví i na prutech 3 a 4
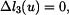 |
(6) |
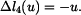 |
(7) |
B. Změny délek od posuvu 
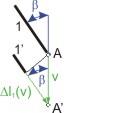 |
Obr.3:Změna délky prutu č.1,způsobená svislým posuvem  |
Na obrázku 3 je znázorněn způsob určení změny délky prutu č.1 , způsobené svislým posuvem  . Dostáváme vztah
. Dostáváme vztah
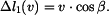 |
(8) |
|
Podobně určíme i další změny délek
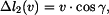 |
(9) |
|
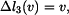 |
(10) |
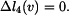 |
(11) |
C. Změny délek způsobené pootočením kolem bodu A
 |
| Obr.4:Smysl pootočení kolem bodu A |
Zvolme si kladný smysl pootočení například podle obrázku 4. Bod A zůstává bez pohybu, proto
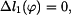 |
(12) |
|
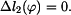 |
(13) |
Bod C se posune svisle o hodnotu 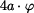 . Platí proto
. Platí proto
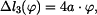 |
(14) |
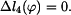 |
(15) |
Na základě rovnic (8) až (15) můžeme souhrně napsat
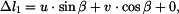 |
(16) |
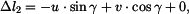 |
(17) |
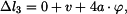 |
(18) |
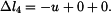 |
(19) |
Pro pruty musejí samozřejmě platit i fyzikální rovnice ve tvaru
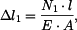 |
(20) |
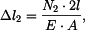 |
(21) |
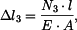 |
(22) |
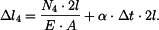 |
(23) |
Vztahy (1) až (3) a (16) až (23) tvoří soustavu jedenácti rovnic pro jedenáct neznámých. Neznámými veličinami jsou: 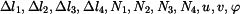 .
.
Zpracoval: František Novotný
Dvakrát osazená tyč v tíhovém poli
Krut - příklady
Příklady z krutu kruhových a mezikruhových průřezů
Dvakrát osazený kroucený hřídel I
 |
 |
| Obr. 1 |
Dáno: 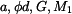
Hřídel je uložen a zatížen podle obr 1.
Určit: reakce, 
Řešení:
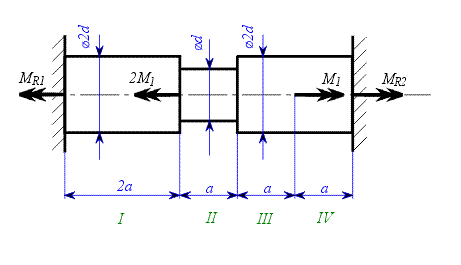 |
 |
| Obr.1 |
Zavedeme reakce např. tak, jako na obr.2 a zapíšeme rovnici rovnováhy:
 , , |
neboli
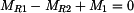 . . |
Úloha je jednou staticky neurčitá. Vzhledem k uložení obou konců můžeme napsat deformační podmínku:
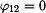 . . |
Metodou řezu nyní stanovíme velikost vnitřního krouticího momentu v úsecích I - IV , jak jsou vyznačeny na obr.2:
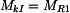 , , |
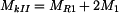 , , |
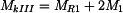 , , |
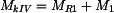 . . |
Polární kvadratické momenty v jednotlivých úsecích hřídele mají hodnoty:
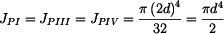 , , |
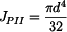 . . |
Vzájemné natočení 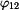 má tvar:
má tvar:
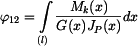 , , |
čili:
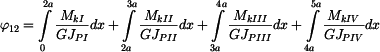 . . |
Po dosazení a integraci dostáváme:
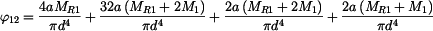 , , |
a po úpravě:
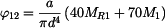 . . |
Dosazením posledního vztahu do deformační rovnice 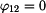 a úpravou dostáváme:
a úpravou dostáváme:
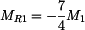 . . |
Z rovnice rovnováhy pak:
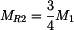 . . |
Pro stanovení napětí nejprve určíme velikost průřezových modulů v krutu 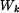 pro
jednotlivé části hřídele.
pro
jednotlivé části hřídele.
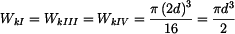 , , |
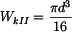 . . |
Smyková napětí pak mají hodnoty:
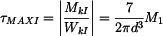 , , |
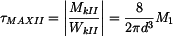 , , |
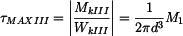 , , |
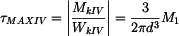 . . |
Pro napětí tedy platí následující relace:
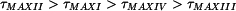 . . |
Největší smykové napětí nabývá hodnoty:
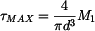 . . |
Hřídel se spojitým kroutícím momentem
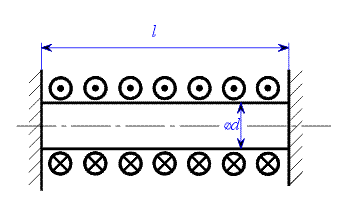 |
 |
| Obr. 1 |
Dáno: 
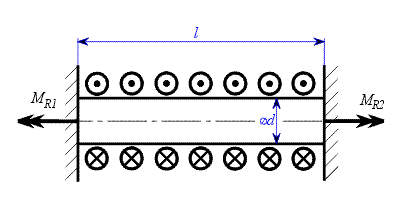
Válcový hřídel je zatížený spojitým krouticím momentem 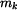 podle obr. 1.
podle obr. 1.
Určit: 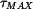
Určete maximální napětí.
Řešení:
 |
 |
| Obr. 2 |
Nejprve zavedeme reakce v uložení např. jako na obr. 2 a zapíšeme rovnici rovnováhy:
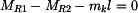 . .
|
(1) |
Úloha je jednou staticky neurčitá. Vzhledem k uložení obou konců má deformační podmínka tvar:
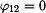 . .
|
(2) |
Metodou řezu stanovíme velikost krouticího momentu na souřadnici x:
 . .
|
(3) |
Pro pootočení 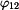 platí:
platí:
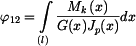 , ,
|
(4) |
což po dosazení a integraci dává:
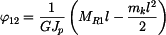 . .
|
(5) |
Dosazením posledního vztahu do deformační podmínky (2) dostaneme:
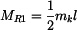 . .
|
(6) |
Z rovnice rovnováhy pak:
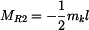 . .
|
(7) |
Vztah (3) po dosazení z (6) nabývá tvaru:
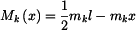 , , |
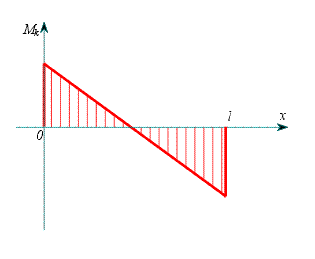
který nám dovolí zakreslit průběh velikosti krouticího momentu - viz obr. 3.
 |
 |
| Obr. 3 |
Krouticí moment nabývá maximální velikosti na obou koncích. Maximální smykové napětí je tedy rovno:
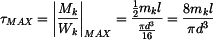 . . |
Zpracoval: Pavel Čapek
Dáno :
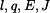
Určete :
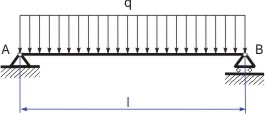
Reakce, průběhy posouvající síly a momentu, tvar průhybové čáry.
Řešení:
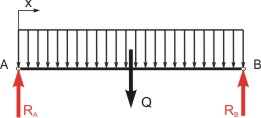 |
| Obr 1: Reakce a výslednice spojitého zatížení |
Nosník uvolníme a zakreslíme reakce (viz obr. 1) a zapíšeme rovnice rovnováhy. Pro rovnice rovnováhy můžeme spojité zatížení nahradit výslednicí 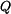 . Její velikost je dána velikostí plochy, charakterizující spojité zatížení
. Její velikost je dána velikostí plochy, charakterizující spojité zatížení 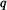 a její působiště je v těžišti této plochy.
a její působiště je v těžišti této plochy.
Rovnice rovnováhy mají tvar
 |
(1) |
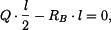 |
(2) |
kde
Reakce mají tedy velikost
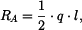 |
(3) |
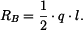 |
(4) |
Posouvající sílu můžeme stanovit například pomocí metody řezu. Zvolme metodu řezu zleva, pro řez v obecném místě  pak platí
pak platí
čili
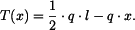 |
(5) |
Metodou řezu určíme i ohybový moment
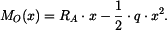 |
(6) |
Reakce  ohýbá nosník v místě
ohýbá nosník v místě  v kladném smyslu (tj. natahuje spodní vlákno nosníku), proto má ve vztahu (6) její moment znaménko plus.
v kladném smyslu (tj. natahuje spodní vlákno nosníku), proto má ve vztahu (6) její moment znaménko plus.
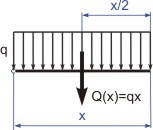 |
| Obr 2: Stanovení momentu od spojitého zatížení |
Na obrázku (2) je znázorněno stanovení ohybového momentu od spojitého zatížení. Vlevo od řezu působí spojité zatížení 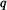 na úsek o délce
na úsek o délce  . Výslednici označme
. Výslednici označme 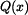 a její velikost je
a její velikost je 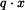 . Působiště výslednice je v těžišti obrazce, tj. ve vzdálenosti
. Působiště výslednice je v těžišti obrazce, tj. ve vzdálenosti 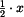 od místa
od místa  . Výsledný moment má tedy velikost
. Výsledný moment má tedy velikost 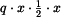 a záporné znaménko, protože zkracuje spodní vlákno nosníku.
a záporné znaménko, protože zkracuje spodní vlákno nosníku.
Pro stanovení tvaru průhybové čáry využijeme diferenciální rovnice ve tvaru
Do čitatele dosadíme z (6) , jmenovatel je konstantní , čili
Po první integraci dostáváme
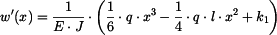 |
(7) |
a po druhé integraci
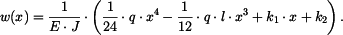 |
(8) |
Hodnoty konstant 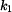 a
a  určíme z okrajových podmínek. Vzhledem k tomu, že nosník je na obou koncích podepřený, musí platit
určíme z okrajových podmínek. Vzhledem k tomu, že nosník je na obou koncích podepřený, musí platit
Dosadíme do (7) a dostaneme
čili
Průhybová čára je určena vztahem
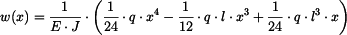 |
(9) |
a sklon
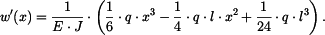 |
(10) |
Vztahy (5), (6), (9), (10) jsou graficky znázorněny na obrázku 3.
Zpracoval: František Novotný
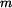 .
.
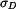 .
Určete prodloužení lana.
.
Určete prodloužení lana.

 o počátku na dolním konci lana a mířící nahoru.
o počátku na dolním konci lana a mířící nahoru.
 a
a 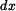 vymezíme infinetisimálně malý element lana.
vymezíme infinetisimálně malý element lana.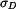 . Element má mimoto ještě vlastní tíhu
. Element má mimoto ještě vlastní tíhu 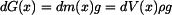 ,
kde
,
kde 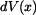 je jeho objem.
je jeho objem.
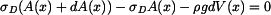 .
.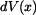 . Můžeme ho rozdělit na válec o objemu
. Můžeme ho rozdělit na válec o objemu 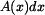 a na část , která tento válec obklopuje.
a na část , která tento válec obklopuje. 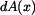 i
i 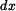 jsou
nekonečně malé veličiny. Objem druhé části bude tak nekonečně malou veličinou 2. řádu a můžeme ho zanedbat.
jsou
nekonečně malé veličiny. Objem druhé části bude tak nekonečně malou veličinou 2. řádu a můžeme ho zanedbat.
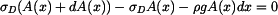 .
.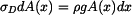 ,
,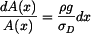 .
. ,
,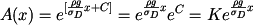 ,
,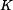 je integrační konstanta.
je integrační konstanta.
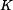 stanovíme z okrajové podmínky. Víme totiž , že i na dolním konci lana
stanovíme z okrajové podmínky. Víme totiž , že i na dolním konci lana 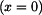 musí být napětí rovno
musí být napětí rovno 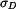 a vnitřní síla v tomto
místě je rovna pouze tíze závaží :
a vnitřní síla v tomto
místě je rovna pouze tíze závaží :
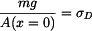 ,
,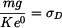
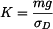 .
.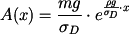 .
.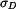 .
.
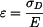
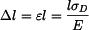 .
.
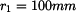
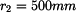
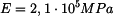
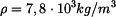
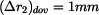
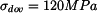
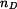 pomocí
pomocí 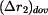 a
a 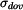 .
.
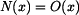
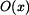 je rovna součinu hmotnosti
je rovna součinu hmotnosti  , poloměru na kterém rotuje těžiště ramene
, poloměru na kterém rotuje těžiště ramene 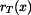 a druhé mocniny úhlové rychlosti
a druhé mocniny úhlové rychlosti
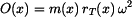 .
. ,
,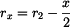 .
.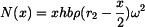 ,
,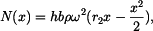
 získáme jako podíl vnitřní síly a průřezu
získáme jako podíl vnitřní síly a průřezu
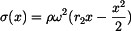
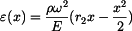 .
.
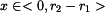 .
.
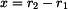 .
.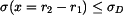 ,
,
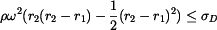 .
.
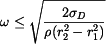 ,
,
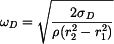 .
.
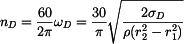 .
.
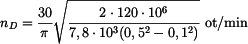
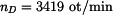 .
.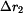 je rovno
je rovno
 ,
,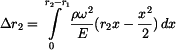 .
.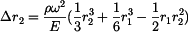 .
.
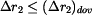 ,
,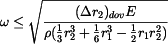
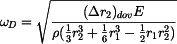 ,
,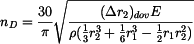 .
.
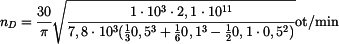
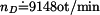 .
.
 .
.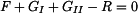 ,
,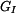 a
a 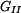 jsou tíhy horní a dolní části sloupu
jsou tíhy horní a dolní části sloupu
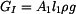
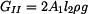 .
.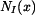 .
.
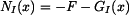 .
.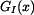 je tíha části sloupu nad řezem
je tíha části sloupu nad řezem
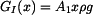 .
.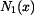 má tedy tvar
má tedy tvar
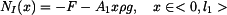 .
.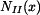 ve spodní části sloupu je dána silou
ve spodní části sloupu je dána silou 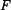 , tíhou celé horní části sloupu
, tíhou celé horní části sloupu 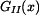 , který se nachází nad myšleným řezem.
, který se nachází nad myšleným řezem.
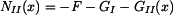 ,
, .
.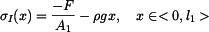
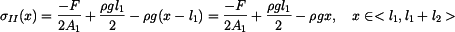 .
.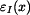 a
a 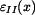 dostaneme z Hookeova zákona
dostaneme z Hookeova zákona
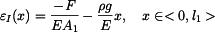
 .
.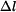 získáme integrací poměrné deformace
získáme integrací poměrné deformace
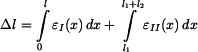 .
.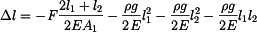 .
.

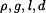 .
.
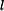 je upevněna podle obr. 1.
je upevněna podle obr. 1.

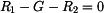 ,
,
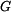 je tíha tyče
je tíha tyče
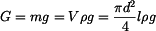 .
.
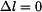 .
.
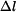 získáme integrací poměrné deformace
získáme integrací poměrné deformace
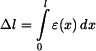 .
.
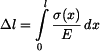
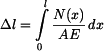 .
.
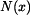 stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici
stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici  , která působí tahem a bude tedy mít kladné znaménko a tíhou
, která působí tahem a bude tedy mít kladné znaménko a tíhou 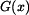 části nad řezem, která působí tlakem a bude tedy mít znaménko mínus.
části nad řezem, která působí tlakem a bude tedy mít znaménko mínus.
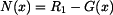 .
.
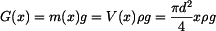 ,
,
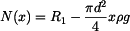 .
.
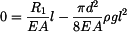 .
.
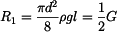 .
.
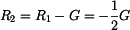 .
.
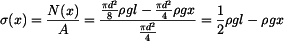 .
.


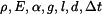 .
.
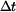 na výsledek.
na výsledek.

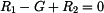 .
.
 se skládá z komponenty způsobené silami
se skládá z komponenty způsobené silami 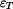 a z komponenty způsobené změnou teploty
a z komponenty způsobené změnou teploty 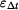 :
:
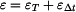 .
.
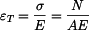 ,
,
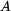 je průřez :
je průřez : 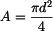 .
.
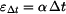 .
.
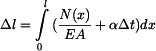 .
.
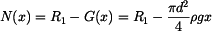 .
.
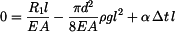 .
.
 .
.
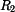 :
:
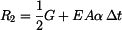 .
.
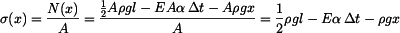 .
.
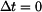 , pak
, pak 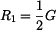 a
a 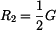 .
.

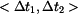 , pak obě reakce míří nahoru. Pro
, pak obě reakce míří nahoru. Pro 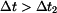 se mění znaménko u
se mění znaménko u 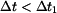 se obrací znaménko a tedy i směr reakce
se obrací znaménko a tedy i směr reakce 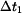 a
a 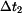 .
.
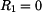 :
:
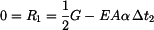 ,
,
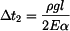 .
.
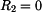 :
:
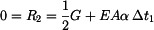
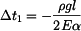 .
.

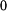 .
.
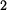 .
.
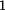 .
.
 , je napětí v části tyče tahové a v části tlakové.
, je napětí v části tyče tahové a v části tlakové.
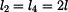
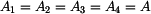
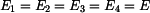
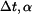


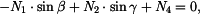
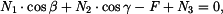
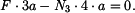
 , svislým posuvem
, svislým posuvem  a pootočením
a pootočením 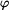 . Každý z těchto vlivů způsobí nějaké změny délek jednotlivých prutů. Skutečná změna délky každého prutu je pak dána jako změny délky od
. Každý z těchto vlivů způsobí nějaké změny délek jednotlivých prutů. Skutečná změna délky každého prutu je pak dána jako změny délky od 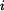 tedy můžeme psát:
tedy můžeme psát:
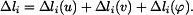

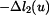 .
.
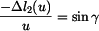
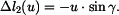
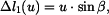
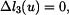
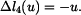

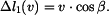
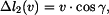
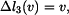
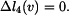
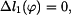
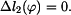
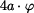 . Platí proto
. Platí proto
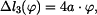
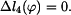
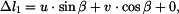
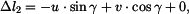
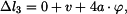
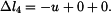
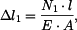
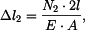
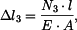
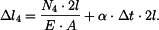
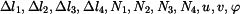 .
.
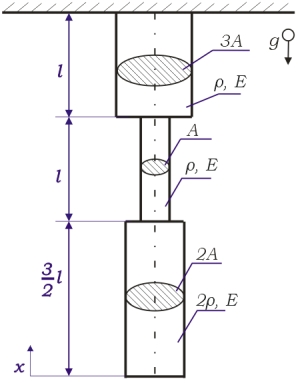
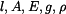
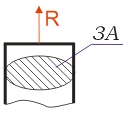
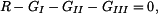
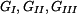 jsou tíhy horní, střední a dolní části tyče
jsou tíhy horní, střední a dolní části tyče
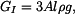
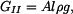
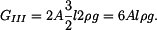
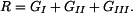
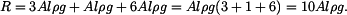
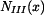
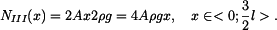
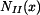 ve střední části tyče je dána tíhou celé spodní části tyče a tíhou fragmentu střední části, která se nachází pod myšleným řezem.
ve střední části tyče je dána tíhou celé spodní části tyče a tíhou fragmentu střední části, která se nachází pod myšleným řezem.
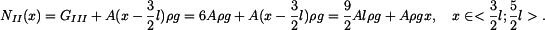
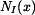 v horní části tyče je dána tíhou spodní a střední části tyče a tíhou fragmentu horní části, která se nachází pod myšleným řezem.
v horní části tyče je dána tíhou spodní a střední části tyče a tíhou fragmentu horní části, která se nachází pod myšleným řezem.
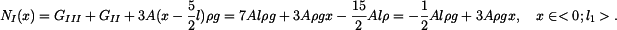
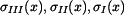 má tvar:
má tvar: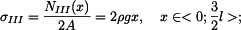
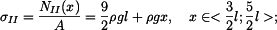
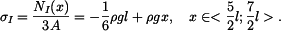
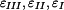 dostaneme z Hookova zákona
dostaneme z Hookova zákona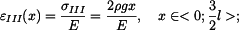
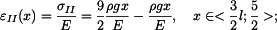
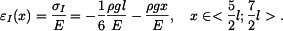
 získáme integrací poměrné deformace
získáme integrací poměrné deformace
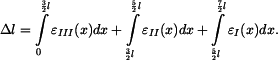

 a napětí
a napětí 
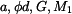


 ,
,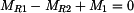 .
.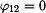 .
.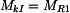 ,
,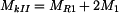 ,
,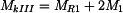 ,
,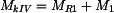 .
.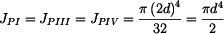 ,
,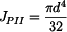 .
.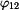 má tvar:
má tvar: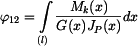 ,
,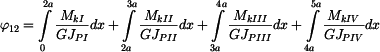 .
.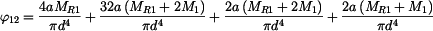 ,
,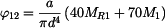 .
.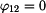 a úpravou dostáváme:
a úpravou dostáváme: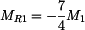 .
.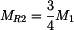 .
.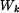 pro
jednotlivé části hřídele.
pro
jednotlivé části hřídele.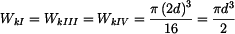 ,
,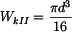 .
.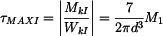 ,
,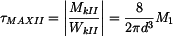 ,
,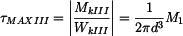 ,
,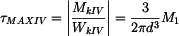 .
.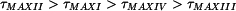 .
.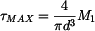 .
.

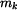 podle obr. 1.
podle obr. 1.
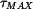

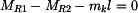 .
.
 .
.
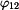 platí:
platí: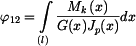 ,
,
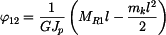 .
.
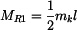 .
.
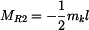 .
.
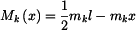 ,
,
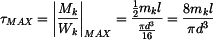 .
.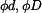
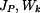
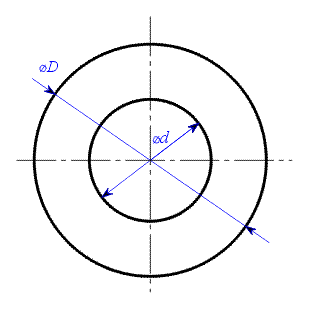
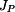 a průřezový modul v krutu
a průřezový modul v krutu 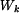 pro kruhový a mezikruhový průřez.
pro kruhový a mezikruhový průřez.
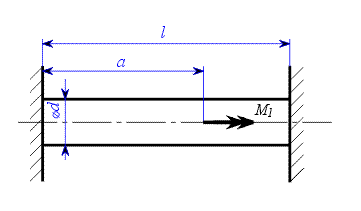
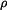 podle obr 1.
podle obr 1. 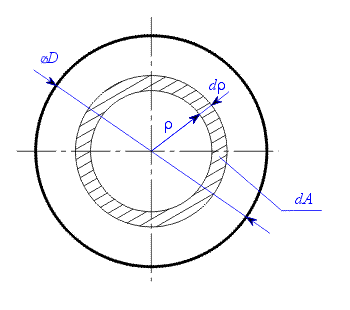
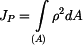 ,
,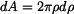 .
.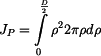 .
.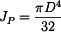 .
.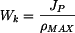 ,
,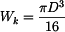 .
.
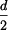 :
: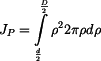 .
.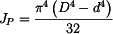 ,
,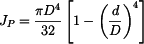 .
.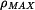 platí
platí 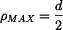 .
.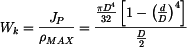 ,
,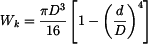 .
.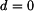 ,
nabyde hranatá závorka hodnoty 1 a získáme vztahy pro kruhový průřez.
,
nabyde hranatá závorka hodnoty 1 a získáme vztahy pro kruhový průřez.
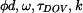
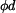 se otáčí úhlovou rychlostí
se otáčí úhlovou rychlostí  .
.
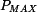
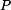 je dán součinem krouticího momentu
je dán součinem krouticího momentu 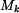 a úhlové rychlosti:
a úhlové rychlosti: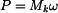 ,
,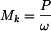 .
.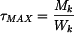 .
.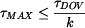 .
.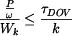 .
.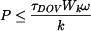 .
.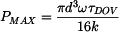 .
.
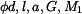
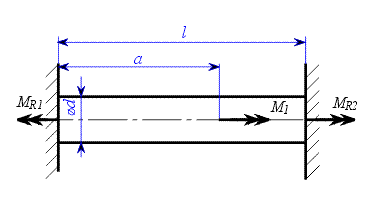
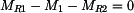 .
.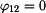 .
.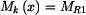 pro
pro
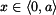 ,
,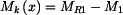 pro
pro
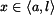 .
.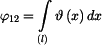 ,
,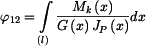 ,
,
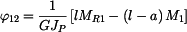 .
.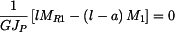
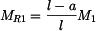 .
.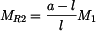 .
.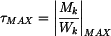 .
.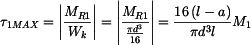
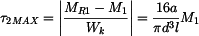 .
.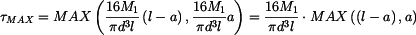 .
.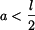 je větší smykové napětí v levé části,
pro
je větší smykové napětí v levé části,
pro 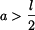 v části pravé.
v části pravé.
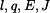

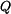 . Její velikost je dána velikostí plochy, charakterizující spojité zatížení
. Její velikost je dána velikostí plochy, charakterizující spojité zatížení 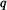 a její působiště je v těžišti této plochy.
a její působiště je v těžišti této plochy.

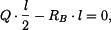
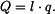
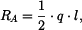
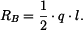
 pak platí
pak platí
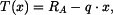
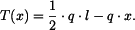
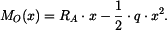
 ohýbá nosník v místě
ohýbá nosník v místě 
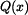 a její velikost je
a její velikost je 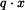 . Působiště výslednice je v těžišti obrazce, tj. ve vzdálenosti
. Působiště výslednice je v těžišti obrazce, tj. ve vzdálenosti 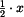 od místa
od místa 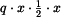 a záporné znaménko, protože zkracuje spodní vlákno nosníku.
a záporné znaménko, protože zkracuje spodní vlákno nosníku.
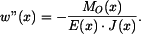
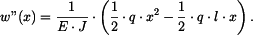
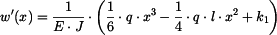
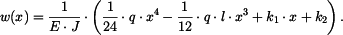
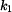 a
a  určíme z okrajových podmínek. Vzhledem k tomu, že nosník je na obou koncích podepřený, musí platit
určíme z okrajových podmínek. Vzhledem k tomu, že nosník je na obou koncích podepřený, musí platit