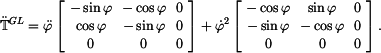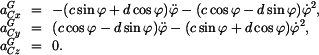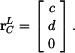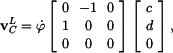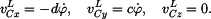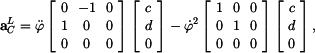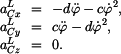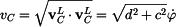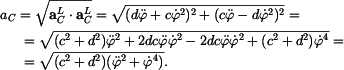|
Navigace |
|
|
|
|
|
|
KIN-07-1 Kinematika zvedacího zařízení
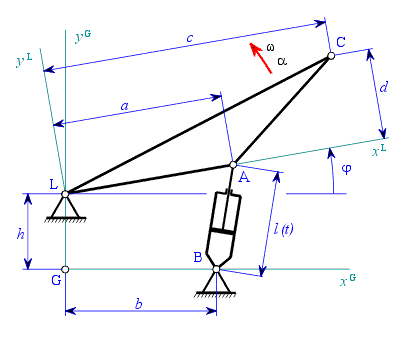
Kinematika zvedacího zařízení podle obrázku.
Dáno:
konstanty
Určit:
kinematické veličiny Řešení: Zavedeme globální a lokální polohové vektory
a napíšeme transformační rovnici pohybu ramene LAC pro bod A
která platí spolu s podmínkou pro vzdálenost
Vzdálenost
přičemž
a skalární součin
Výsledek dosadíme do druhé mocniny podmínky (1) a máme
Upravíme na tvar
To je tzv. úplná rovnice trigonometrická typu
Taková rovnice se řeší substitucí
která danou rovnici převede na tvar
resp.
s řešením
Potom obě rovnice (4) povýšíma na druhou a sečteme
(znaménko + nebo - se vybere tak, aby řešení odpovídalo zadání). Nakonec je tedy řešení rovnice (3)
V našem případě je
takže
Druhý člen je
což je úhel BLG, který je rozhodně větší než úhel
Úhlová rychlost
Protože by bylo pracné derivovat (6), použijeme implicitní derivaci vztahu (2) s přihlédnutím k tomu, že
takže
přičemž za
Úhlové zrychlení
Opět nebudeme derivovat přímo (8), ale implicitně jednodušší vztah (7) s výsledkem
takže
Kinematické veličiny bodu C v GSS: Použijeme transformační rovnici pro bod C
neboli
Z toho složky polohového vektoru v GSS
Vektor rychlosti v GSS dostaneme derivováním (9). Protože
Derivace matice je matice derivovaných členů. Neboli
Z toho složky vektoru rychlosti v GSS
Vektor zrychení v GSS dostaneme dalším derivováním (10). Dostaneme
Druhá derivace
Po vynásobení vektorem
(Ke stejnému výsledku bychom samozřejmě došli i přímým derivování rovnic(11)). V LSS je polohový vektor bodu C zadán
Pro určení vektoru rychlosti použijeme výsledek z přednášky
takže
Podobně výsledky z přednášky pro vektor zrychlení v LSS dávají
takže
Nakonec vypočteme absolutní hodnoty(velikosti) vektorů rychlosti a zrychlení. Ty jsou stejné bez ohledu na použitý SS; použijeme proto lokální, protože složky zde vycházejí jednodušší. Je tedy
a
|
|
|
|
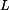 ,
,  ; rozměry
; rozměry  ,
, 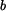 ,
,  ,
, 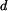 ,
, 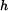 ; závislost
; závislost
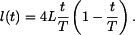
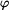 ,
,  ,
,  rotačního pohybu tělesa LAC; kinematické veličiny
rotačního pohybu tělesa LAC; kinematické veličiny
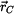 ,
, 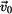 ,
, 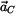 v GSS
v GSS 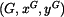 a v LSS
a v LSS 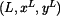 .
.
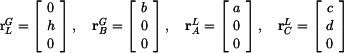
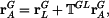
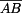 ve tvaru,
ve tvaru,
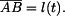
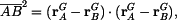
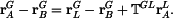
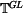 je zde transformační matice pro rotaci okolo osy
je zde transformační matice pro rotaci okolo osy 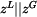 , takže platí
, takže platí
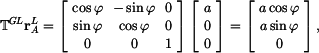
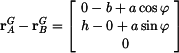
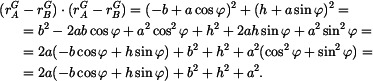
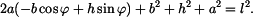
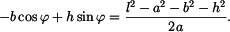
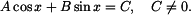
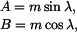
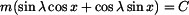
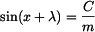
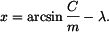
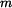 a
a 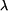 určíma řešením soustavy (4). Nejprve rovnice dělíme, takže
určíma řešením soustavy (4). Nejprve rovnice dělíme, takže

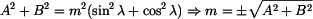

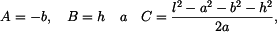

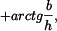
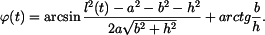
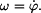
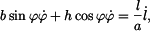

 můžeme dosadit podle zadání
můžeme dosadit podle zadání
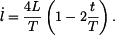
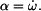
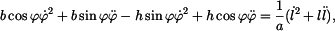
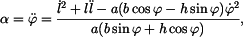
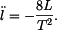
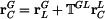
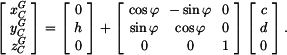

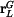 a
a 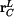 jsou konstantní, platí
jsou konstantní, platí
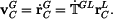
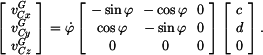
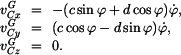
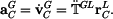
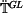 transformační matice se skládá ze dvou členů
transformační matice se skládá ze dvou členů