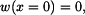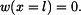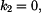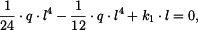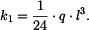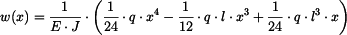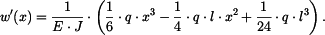|
Navigace |
|
|
|
|
|
|
|
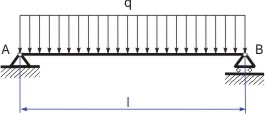
Nosník na dvou podporách s konstantním spojitým zatížením
Dáno :
Určete : Reakce, průběhy posouvající síly a momentu, tvar průhybové čáry. Řešení:
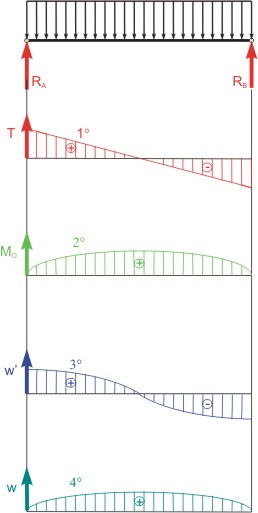
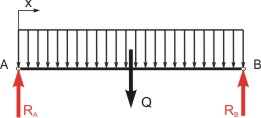
Nosník uvolníme a zakreslíme reakce (viz obr. 1) a zapíšeme rovnice rovnováhy. Pro rovnice rovnováhy můžeme spojité zatížení nahradit výslednicí Rovnice rovnováhy mají tvar
kde
Reakce mají tedy velikost
Posouvající sílu můžeme stanovit například pomocí metody řezu. Zvolme metodu řezu zleva, pro řez v obecném místě
čili
Metodou řezu určíme i ohybový moment
Reakce
Na obrázku (2) je znázorněno stanovení ohybového momentu od spojitého zatížení. Vlevo od řezu působí spojité zatížení Pro stanovení tvaru průhybové čáry využijeme diferenciální rovnice ve tvaru
Do čitatele dosadíme z (6) , jmenovatel je konstantní , čili
Po první integraci dostáváme
a po druhé integraci
Hodnoty konstant
Dosadíme do (7) a dostaneme
čili
Průhybová čára je určena vztahem
a sklon
Vztahy (5), (6), (9), (10) jsou graficky znázorněny na obrázku 3.
Zpracoval: František Novotný |
|
|
|
|
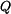 . Její velikost je dána velikostí plochy, charakterizující spojité zatížení
. Její velikost je dána velikostí plochy, charakterizující spojité zatížení 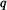 a její působiště je v těžišti této plochy.
a její působiště je v těžišti této plochy.

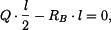
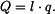
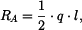
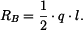
 pak platí
pak platí
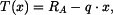
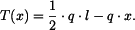
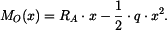
 ohýbá nosník v místě
ohýbá nosník v místě 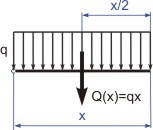
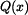 a její velikost je
a její velikost je 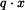 . Působiště výslednice je v těžišti obrazce, tj. ve vzdálenosti
. Působiště výslednice je v těžišti obrazce, tj. ve vzdálenosti 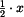 od místa
od místa 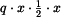 a záporné znaménko, protože zkracuje spodní vlákno nosníku.
a záporné znaménko, protože zkracuje spodní vlákno nosníku.
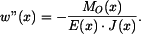
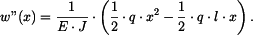
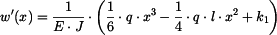
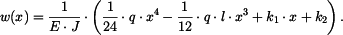
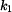 a
a  určíme z okrajových podmínek. Vzhledem k tomu, že nosník je na obou koncích podepřený, musí platit
určíme z okrajových podmínek. Vzhledem k tomu, že nosník je na obou koncích podepřený, musí platit