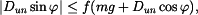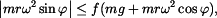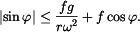|
Navigace |
|
|
|
|
|
|
Hmotný bod na paralelogramu
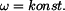 , , 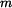 , ,  , , 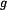 , , 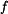
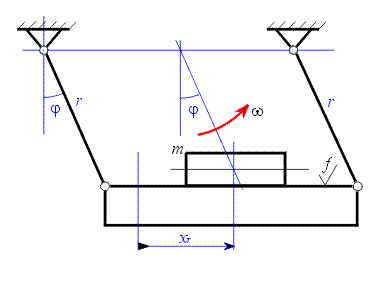
Je dán paralelogram rotující s konstantní úhlovou rychlostí
Určit: podmínky pohybu hmotného bodu
Určete podmínky pohybu hmotného bodu po tělese paralelogramu.
Řešení:
K řešení použijeme uvolňovací metodu v kombinaci s D'Alembertovým způsobem vyjádření setrvačných účinků.
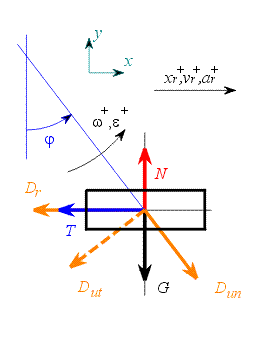
Unášivý pohyb koná těleso paralelogramu. Je to pohyb posuvný. Relativní pohyb bodu po paralelogramu je taktéž posuvný.
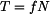 je třecí síla mezi hmotným bodem a tělesem paralelogramu,
je třecí síla mezi hmotným bodem a tělesem paralelogramu,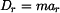 je D'Alembertova doplňková síla relativního pohybu,
je D'Alembertova doplňková síla relativního pohybu,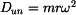 je D'Alembertova doplňková síla unášivého pohybu.
je D'Alembertova doplňková síla unášivého pohybu.
V tomto případě jde pouze o složku normálovou (odstředivou).
Složka tečná (na obr. 2 znázorněna čárkovaně)
Podmínka pro styk bodu a tělesa je nenulová normálová síla (v mezním případě může být i nulová). Je vidět, že síla
Odtud můžeme vyjádřit:
Parametry
2) Oblast relativního pohybu hmotného bodu
Absolutní hodnota na levé straně znamená, že abstrahujeme od směru relativního pohybu. Zajímá nás pouze informace, zda bod vzhledem k tělesu paralelogramu stojí nebo ne. Je-li relativní rychlost
a odtud
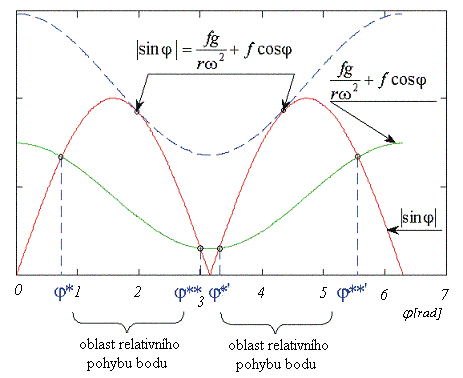
Podmínka (5) říká, že pokud úhel 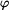 nabývá takové hodnoty, že absolutní hodnota jeho sinu je menší (maximálně rovna) než pravá strana rovnice,
potom nedochází k relativnímu pohybu bodu po tělese paralelogramu. To je graficky vyjádřeno na obrázku. Bod se v oblasti nabývá takové hodnoty, že absolutní hodnota jeho sinu je menší (maximálně rovna) než pravá strana rovnice,
potom nedochází k relativnímu pohybu bodu po tělese paralelogramu. To je graficky vyjádřeno na obrázku. Bod se v oblasti
 nebo symetricky
nebo symetricky
 nepohybuje. Přesáhnou-li funkční hodnoty pravé strany (5) na celém intervalu
nepohybuje. Přesáhnou-li funkční hodnoty pravé strany (5) na celém intervalu
 mezní čárkovanou křivku, která má s křivkou levé strany pouze dva
společné body, potom k pohybu bodu nedojde nikdy.
mezní čárkovanou křivku, která má s křivkou levé strany pouze dva
společné body, potom k pohybu bodu nedojde nikdy.
|
|
|
|
 .
Na tělese paralelogramu je umístěn hmotný bod o hmotnosti
.
Na tělese paralelogramu je umístěn hmotný bod o hmotnosti  .
. 
 a
a 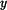 :
:
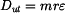 je nulová , protože
je nulová , protože 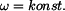 , tedy
, tedy 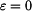 .
.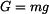 je tíhová síla působící na hmotný bod,
je tíhová síla působící na hmotný bod,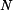 je síla normálová.
je síla normálová.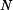 .
.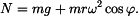
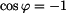 . Tzn., že úhel
. Tzn., že úhel
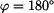 je pro možnost ztráty kontaktu s podložkou kritickým místem. Podmínka nepřetržitého styku bodu a tělesa tedy je:
je pro možnost ztráty kontaktu s podložkou kritickým místem. Podmínka nepřetržitého styku bodu a tělesa tedy je: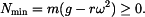
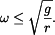
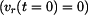 .
Budeme zkoumat, za jakých podmínek nedojde k posunu bodu po tělese.
.
Budeme zkoumat, za jakých podmínek nedojde k posunu bodu po tělese.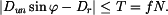
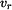 nulová, a nemá-li se
tento stav změnit, musí být relativní zrychlení
nulová, a nemá-li se
tento stav změnit, musí být relativní zrychlení 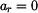 a tím i D'Alembertova doplňková síla relativního pohybu
a tím i D'Alembertova doplňková síla relativního pohybu 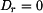 . Proto rovnici (4) můžeme po dosazení za
. Proto rovnici (4) můžeme po dosazení za 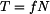 a užití (2)
přepsat do tvaru:
a užití (2)
přepsat do tvaru: