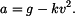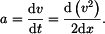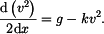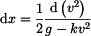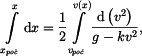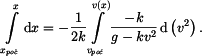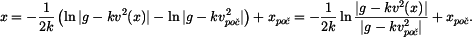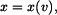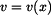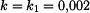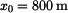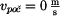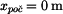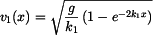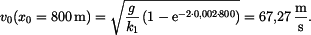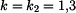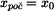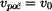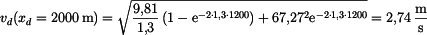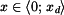|
Seskok parašutisty v odporujícím prostředí
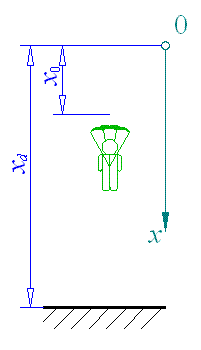
Z letadla letícího ve výšce  seskočí parašutista. seskočí parašutista.
- V intervalu
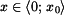 letí parašutista rychlostí letí parašutista rychlostí 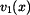 volným pádem, kde na něj působí odpor vzduchu. Součinitel odporu vzduchu je volným pádem, kde na něj působí odpor vzduchu. Součinitel odporu vzduchu je 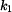 . .
- Ve výšce
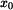 otevře padák, čímž velmi zvětší odpor vzduchu na otevře padák, čímž velmi zvětší odpor vzduchu na 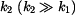 . Parašutista letí rychlostí . Parašutista letí rychlostí 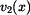 . .
Sestavíme diferenciální rovnici
Tuto rovnici vyřešíme metodou separace proměnných
a dále aplikací určitých integrálů
kde 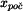 jako dolní mez integrálu je obecně dráha při započetí děje s počáteční rychlostí jako dolní mez integrálu je obecně dráha při započetí děje s počáteční rychlostí 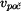 . Po rozšíření pravé strany zlomkem . Po rozšíření pravé strany zlomkem 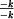 a malé úpravě lze použít pravidlo o integrování zlomku, kdy v čitateli je derivace jmenovatele. Potom je integrálem tohoto zlomku logaritmus jmenovatele.
Po integraci dostaneme
Nyní máme funkci
z ní určíme funkci inverzní
a obdržíme řešení v obecném tvaru a malé úpravě lze použít pravidlo o integrování zlomku, kdy v čitateli je derivace jmenovatele. Potom je integrálem tohoto zlomku logaritmus jmenovatele.
Po integraci dostaneme
Nyní máme funkci
z ní určíme funkci inverzní
a obdržíme řešení v obecném tvaru
Řešení pro konkrétní případ
1.fáze - volný pád parašutisty bez padáku
- součinitel odporu vzduchu je např.
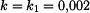
- délka volného pádu
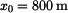
- počáteční rychlost seskoku
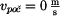
- počáteční poloha děje
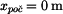
vztah se v tomto případě zjednoduší na
2.fáze - pád s otevřeným padákem
- součinitel odporu vzduchu při otevřeném padáku je např.
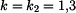
- počáteční poloha děje
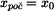
- počáteční rychlost děje
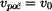
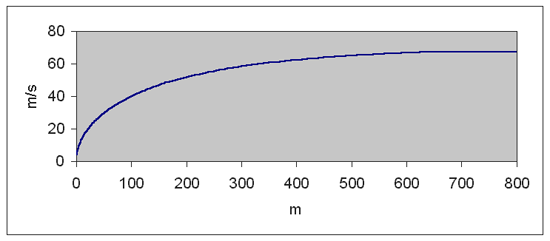
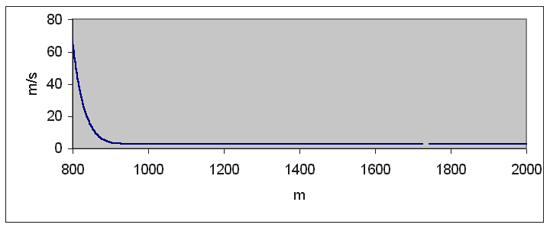
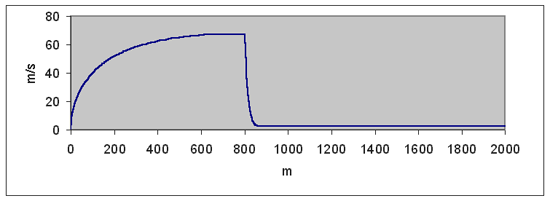
Průběh rychlosti parašutisty v celém intervalu 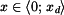
Soubory ke stažení
Výpočový program v MathCadu:
 para.mcd - MathCad v.2000 para.mcd - MathCad v.2000
 para6.mcd - MathCad v.6 para6.mcd - MathCad v.6
|
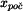 jako dolní mez integrálu je obecně dráha při započetí děje s počáteční rychlostí
jako dolní mez integrálu je obecně dráha při započetí děje s počáteční rychlostí 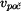 . Po rozšíření pravé strany zlomkem
. Po rozšíření pravé strany zlomkem 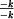 a malé úpravě lze použít pravidlo o integrování zlomku, kdy v čitateli je derivace jmenovatele. Potom je integrálem tohoto zlomku logaritmus jmenovatele.
a malé úpravě lze použít pravidlo o integrování zlomku, kdy v čitateli je derivace jmenovatele. Potom je integrálem tohoto zlomku logaritmus jmenovatele.
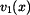 ,
, 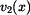
 seskočí parašutista.
seskočí parašutista.
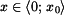 letí parašutista rychlostí
letí parašutista rychlostí 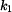 .
.
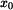 otevře padák, čímž velmi zvětší odpor vzduchu na
otevře padák, čímž velmi zvětší odpor vzduchu na 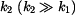 . Parašutista letí rychlostí
. Parašutista letí rychlostí  ,
, 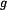 ,
, 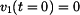 .
.
 v obou intervalech, tj.
v obou intervalech, tj. 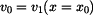 , a jakou rychlostí
, a jakou rychlostí 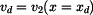 dopadne parašutista na zem.
dopadne parašutista na zem.