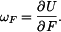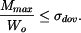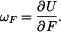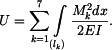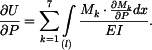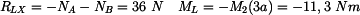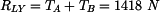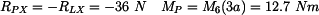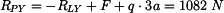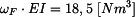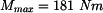|
Navigace |
|
|
|
|
|
|
Rám namáhaný na ohyb
Upozorneni: v tabulce momentu v radku 3 ma byt znamenko + mezi prvnim a druhym clenem. Brzy opravim. Prilozeny Matlabovsky skript a vysledky jsou vporadku. Marvalova 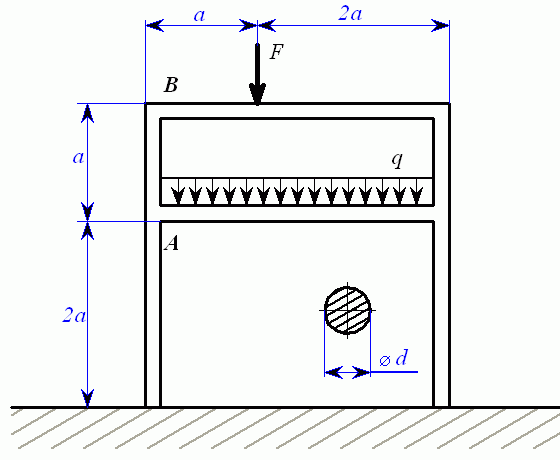
Rám z materiálu s modulem pružnosti Dáno: 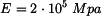 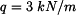 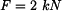 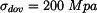 Určit: 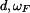 Řešení: Průbyb určíme pomocí Castiglianovy věty:
Pro určení průřezu musíme vypočítat maxilmální vnitřní ohybový moment a průřez určíme z podmínky:
Jde o uzavřený rám, u kterého musíme nejprve určit vnitřní síly ve dvou vhodně zvolených myšlených řezech, máme tedy 6 nezávislých neznámých vnitřních sil. Možností jak zvolit tyto dva řezy je celá řada, rám by jimi měl být rozdělen na dvě staticky určité části. Jednou z možností je oddělit příčku v bodě A a rozdělit rám na dvě části v levém horním rohu B. 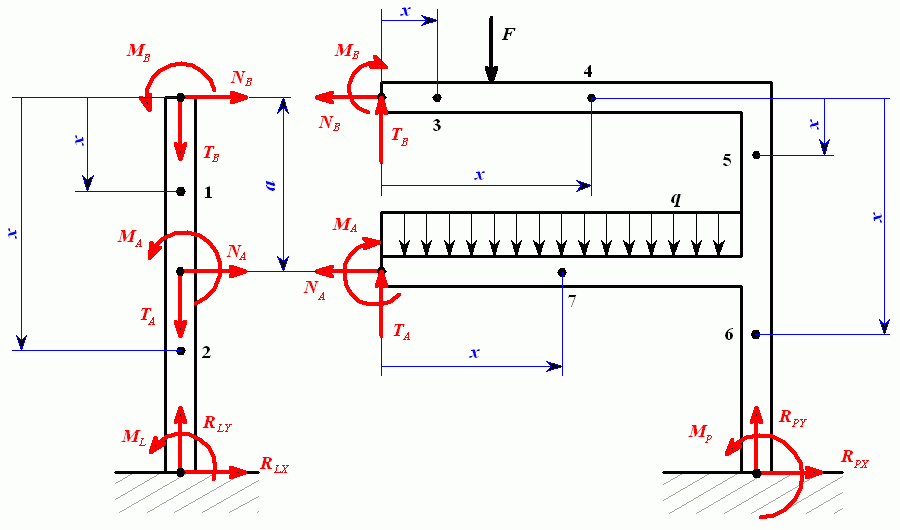
V řezu A i B působí momenty 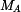 a a 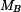 a dvě složky síly označené a dvě složky síly označené 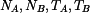 . Tyto síly jsou staticky neurčité - zapíšeme podmínky pro minimum deformační energie - šest rovnic pro šest neznámých: . Tyto síly jsou staticky neurčité - zapíšeme podmínky pro minimum deformační energie - šest rovnic pro šest neznámých:
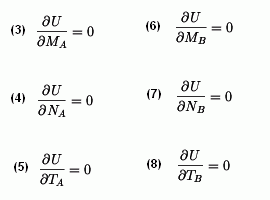
K těmto rovnicím připojíme ještě rovnici (1) pro výpočet průbybu pod silou F.
Levé strany těchto rovnic rozepíšeme. Rám je namáhán převážně na ohyb, budeme uvažovat pouze deformační energii od ohybových napětí. Rám rozdělíme na úseky, ve kterých je vnitřní ohybový moment spojitou funkcí souřadnic. Hranice těchto úseků jsou v rozích a v místech, kde působí osamělé síly. Rám je tedy třeba rozdělit na 7 úseků. Celková doformační energie je součtem deformační energie v jednotlivých částech rámu:
Derivace U podle síly P, kde P je postupně 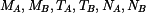 a a 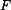 : :
Je tedy třeba určit vnitřní ohybové momenty v jednotlivých částech a jejich derivace vzhledem k jednotlivým silám. 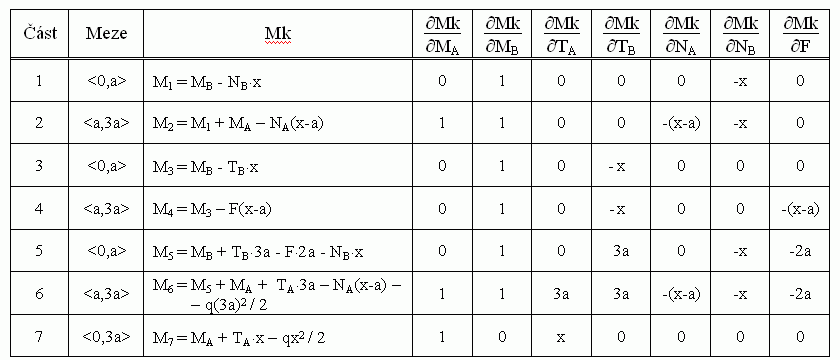
Nyní máme vše připraveno k dosazení do rovnic (1) a (3 ÷ 8). Sloupec momentů v tabulce vynásobíme sloupcem příslušné derivace a integrujeme v daných mezích, integrály sečteme. Soustavu sedmi rovnic vyřešíme a vypočtené síly dosadíme zpět do vztahů pro momenty 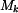 . Určíme maximální moment. Vnitřní momenty jsou v částech 1 ÷ 6 lineární funkcí x, maxima mohou být buď na počátku, nebo na konci úseku. v příčce je moment kvadratickou funkcí x, jeho maximum může být buď na počátku či na konci příčky, nebo ve vrcholu paraboly. Určíme ho obvyklým způsobem. Momenty zakreslíme do grafů. . Určíme maximální moment. Vnitřní momenty jsou v částech 1 ÷ 6 lineární funkcí x, maxima mohou být buď na počátku, nebo na konci úseku. v příčce je moment kvadratickou funkcí x, jeho maximum může být buď na počátku či na konci příčky, nebo ve vrcholu paraboly. Určíme ho obvyklým způsobem. Momenty zakreslíme do grafů.
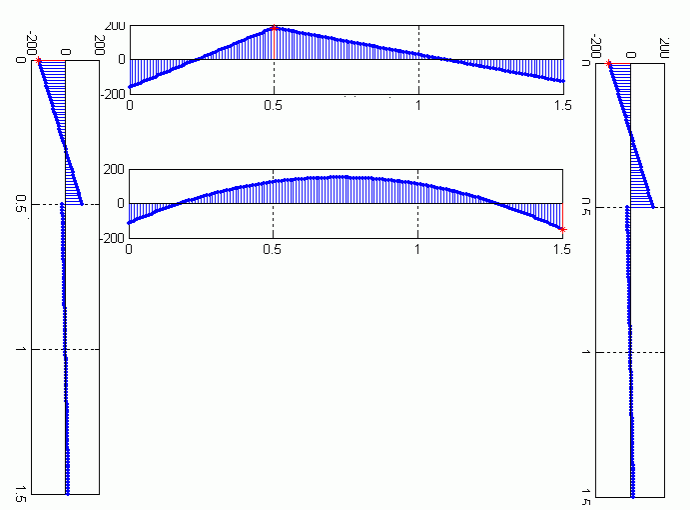
Určíme také reakce ve vetknutích. Levé vetknutí:
Pravé vetknutí:
Průhyb pod silou F bude:
Maximální vnitřní moment je pod silou F a jeho hodnota je:
Určíme průměr průřezu rámu ze vztahu (2) a dosadíme do vztahu pro průhyb. Řešení úlohy je dosti pracné, avšak ve chvíli, kdy jsme sestavili tabulku 1, můžeme svěřit výpočet počítači. K příkladu je přiložen textový soubor, který lze zkopírovat, uložit příponou .m (file.m) a spustit v prostředí MATLAB. Program využívá SYMBOLIC TOOLBOX. Skript si jistě MATLABu znalí studenti dokáží sestavit mnohem racionálněji. Z grafů vnitřních momentů, které jsou jedním z výstupů výpočtu, vidíme, že rám je nejvíce namáhán v horní uzavřené části. Dolní části stojanu jsou namáhány tlakem - přenáší zatížení do podpor. Momenty ve vetknutích jsou o řád menší, než maximální moment. Zpracoval: Zozulák Petr |
|
|
|
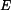 má konstantní průřez
má konstantní průřez 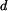 . Je zatížen spojitým zatížením
. Je zatížen spojitým zatížením 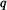 a osamělou silou
a osamělou silou