|
Navigace |
|
|
|
|
|
|
|
Průřezové veličiny kroucené tyče uzavřeného tenkostěnného průřezu.
Dáno: 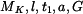 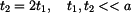
Tyč tenkostěnného průřezu podle obr. 1 je zatížena kroutícím momentem
Určit:
Určete průřezový modul v krutu
Řešení:
Řešíme pomocí fiktivního experimentu na tenké membráně namáhané fiktivním tlakem
V průřezu vznikají dvě velikosti napětí (podle 2. věty membránové analogie), která jsou po tloušťce
Podle 3. věty membránové analogie platí :
Maximální napětí
odkud plyne
Protože platí :
je
Ze čtvrté věty membránové analogie určíme
Výraz
Odtud :
Po dosazení za
Maximální napětí vzniká ve dvou stranách o tloušťce
Vzájemné pootočení koncových průřezů je :
|
|
|
|
|
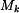
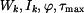
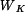 , moment tuhosti
, moment tuhosti 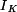 , pootočení koncových průřezů tyče, maximální napětí
, pootočení koncových průřezů tyče, maximální napětí 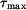 a místo průřezu v němž působí.
a místo průřezu v němž působí.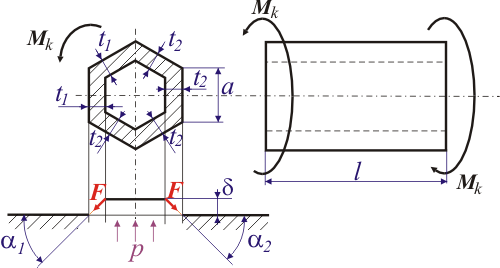
 (představa o experimentu je znázorněna ve spodní části obr.1).
(představa o experimentu je znázorněna ve spodní části obr.1).
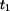 příp.
příp. 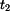 přibližně konstantní.
přibližně konstantní.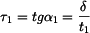
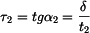
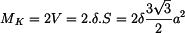
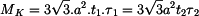
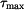 určíme porovnáním obou napětí
určíme porovnáním obou napětí 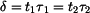
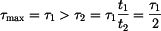
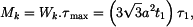
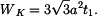
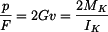
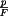 získáme z rovnice rovnováhy vložené destičky experimentu
získáme z rovnice rovnováhy vložené destičky experimentu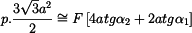
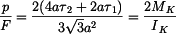
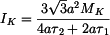
 a
a 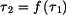 se
se 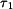 ve výrazu zkrátí a vyjde :
ve výrazu zkrátí a vyjde :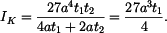
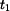 a délce
a délce  šestiúhelníkového průřezu trubky :
šestiúhelníkového průřezu trubky :