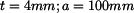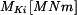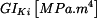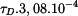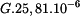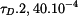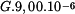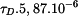|
Navigace |
|
|
|
|
|
|
Průřezové veličiny různých variant tenkostěnného průřezu. Srovnání jejich tuhosti a únosnosti.
Dáno: 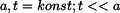
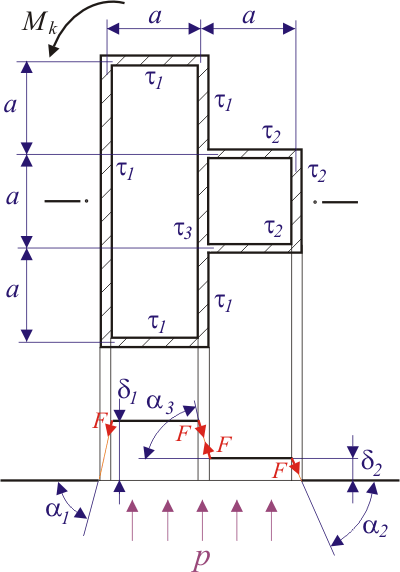
Jsou dány tyče tenkostěnného průřezu (uzavřený průřez s dvojnásobně souvislou oblastí, uzavřený průřez s žebry a otevřený průřez) namáhané na krut.
Určit:
Určete průřezové moduly v krutu
Řešení: I. Průřez s dvojnásobně souvislou oblastí: V průřezu vznikají napětí
Podle třetí věty membránové analogie platí :
Vzájemné vztahy mezi napětími z rovnic rovnováhy obou vložených destiček (pro malé úhly
Po dosazení z první a druhé rovnice rovnováhy vyjde
Odtud dostaneme :
a tedy platí, že
Rovnice pro kroutící moment
takže
Dále podle čtvrté věty membránové analogie je
Odtud :
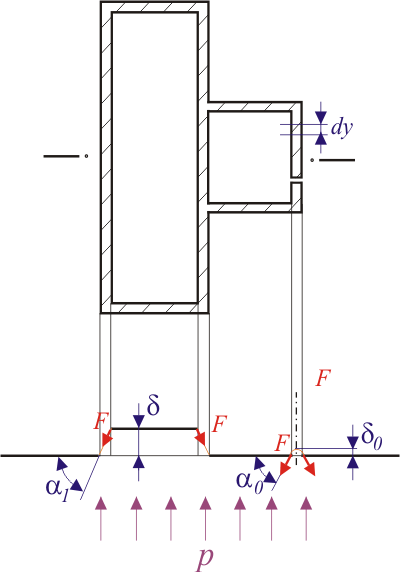
II. Rozřízneme-li kroucenou tyč po délce podle obr. 2, získáme uzavřený profil s žebry
V průřezu vzniknou napětí :
Podle třetí věty membránové analogie lze napsat:
Po dosazení je
Z rovnic rovnováhy vložené destičky a části membrány o délce
Vyjde:
a protože
a tedy
Moment tuhosti v krutu je :
III. Rozřízneme-li tyč po její délce ve dvou místech podle obr. 3, dostaneme otevřený profil.
Průřezové veličiny určíme ze vztahů :
Srovnání únosnosti
Uzavřené profily mají (řádově) výrazně větší únosnost a tuhost nežli otevřené. |
|
|
|
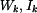
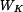 a momenty tuhosti v krutu
a momenty tuhosti v krutu 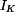 průřezů podle obr. 1, 2, 3. Srovnejte jejich únosnost a tuhost.
průřezů podle obr. 1, 2, 3. Srovnejte jejich únosnost a tuhost.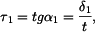
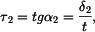
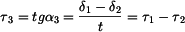
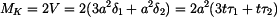
 platí
platí 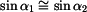 atd. ):
atd. ):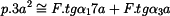
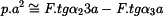
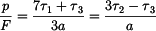
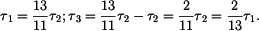
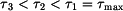
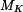 upravíme do tvaru :
upravíme do tvaru :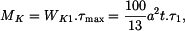

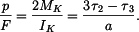
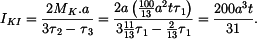
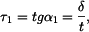
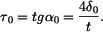
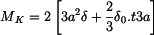
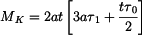
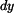
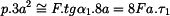
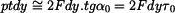
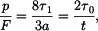
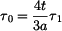
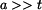 je
je 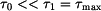 .
Do rovnice pro
.
Do rovnice pro 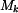 dosadíme za
dosadíme za 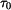
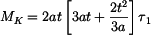
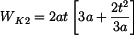
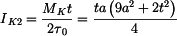

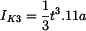
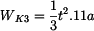
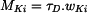 a tuhosti
a tuhosti 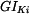 průřezů podle obr. 1, 2, 3 pro dovolené napětí
průřezů podle obr. 1, 2, 3 pro dovolené napětí 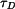 pro velikost průřezu
pro velikost průřezu