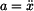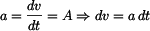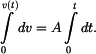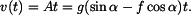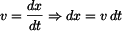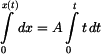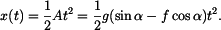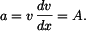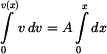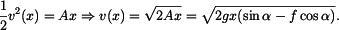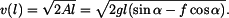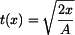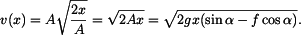|
Navigace |
|
|
|
|
|
|
Hmotný bod na drsné nakloněné rovině
Dáno: 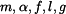 Je dán bod o hmotnosti 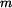 na drsné rovině skloněné pod úhlem na drsné rovině skloněné pod úhlem  . Rychlost a poloha bodu na počátku děje
jsou nulové. Bod je uveden do pohybu vlivem vlastní tíže. Koeficient tření mezi bodem a rovinou je . Rychlost a poloha bodu na počátku děje
jsou nulové. Bod je uveden do pohybu vlivem vlastní tíže. Koeficient tření mezi bodem a rovinou je 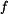 . .Určit: 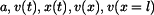 Určete zrychlení, rychlost a polohu bodu v závislosti na čase, rychlost bodu v závislosti na dráze a rychlost bodu po překonání vzdálenosti 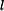 . .Rešení:
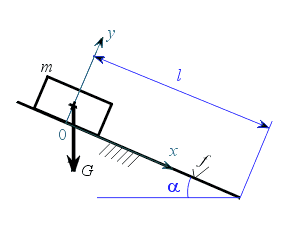
Na obrázku je zachyceno uvolnění bodu v obecné poloze. K sestavení pohybové rovnice užijeme Newtonova způsobu. Ve vektorovém vyjádření platí :
Složkové rovnice psané ve směru osy  a a 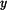 jsou : jsou :
kde je 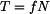 třecí síla, třecí síla,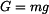 tíhová síla. tíhová síla. Z rovnice (2) vyjádříme normálovou sílu 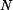 a dosadíme do (1). a dosadíme do (1).
Rovnici (1) vydělíme hmotností 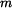 a přepíšeme do tvaru : a přepíšeme do tvaru :
Dostali jsme hlavní pohybovou rovnici (3) . Je to lineární diferenciální rovnice 2.řádu s nenulovou pravou stranou. Zrychlení bodu  je závislé na parametrech je závislé na parametrech 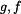 a a  . To jsou ale z hlediska zadání konstanty. Tedy i výsledné
zrychlení je konstantní a označíme jej . To jsou ale z hlediska zadání konstanty. Tedy i výsledné
zrychlení je konstantní a označíme jej 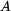 . .Rychlost bodu v závislosti na čase ; 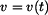 : :
Vzhledem k jednoduchosti rovnice (3) lze k řešení použít separaci proměnných a poté integrovat. Jako spodní meze intervalu nám poslouží příslušné počáteční podmínky. V tomto případě 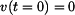 . Do horních mezí použijeme obecné hodnoty
rychlosti . Do horních mezí použijeme obecné hodnoty
rychlosti 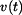 a času a času 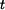 . .
Po integraci :
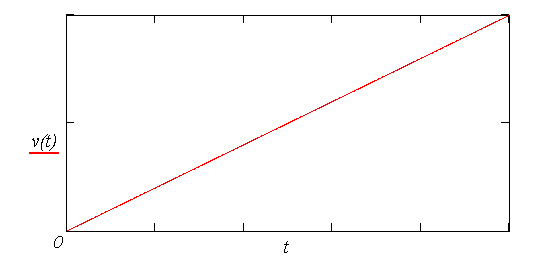
Rychlost na čase závisí lineárně. Poloha v závislosti na čase ;  : :Užijeme obdobného postupu jako při řešení rychlosti. Počáteční podmínka v dolních mezích integrálů je 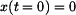 . .
Po integraci :
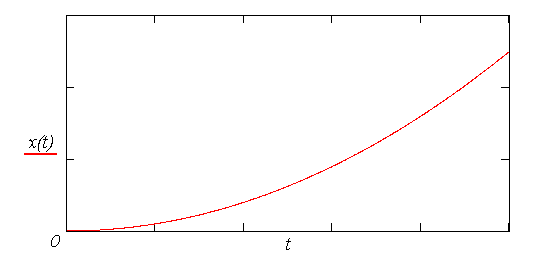
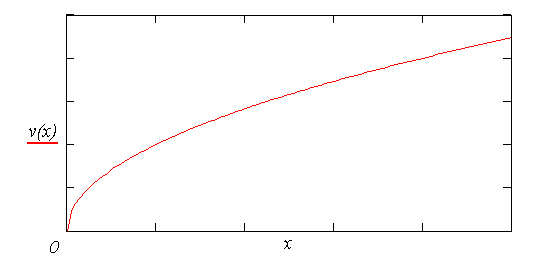
Poloha je tedy z hlediska času funkce kvadratická. Rychlost bodu v závislosti na poloze ; 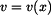 : :K výpočtu lze například využít vztahu :
Počáteční podmínka užitá ve spodních mezích integrálů je 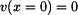 . .
Hodnota rychlosti v okamžiku dosažení dráhy 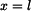 je je
Stejného výsledku lze při určování závislosti 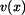 dosáhnout tak , že z rovnice (5) vyjádříme čas v závislosti na dráze : dosáhnout tak , že z rovnice (5) vyjádříme čas v závislosti na dráze :
a dosadíme do (4) :
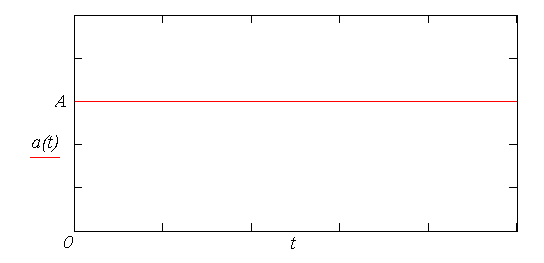
Grafické průběhy vypočtených závislostí jsou na obr. 3 až obr. 6. Zrychlení bodu 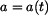
Rychlost bodu 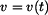
Poloha bodu 
Rychlost bodu 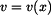
|
|
|
|
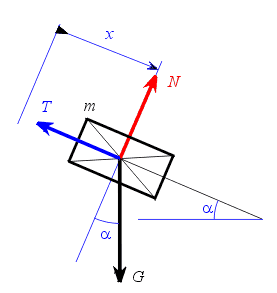
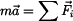
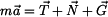
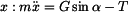
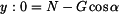 ,
,
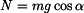
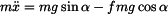
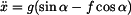 ,
,