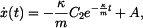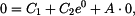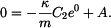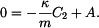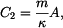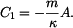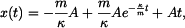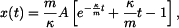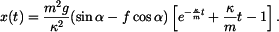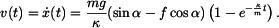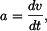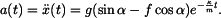|
Navigace |
|
|
|
|
|
|
Hmotný bod na drsné nakloněné rovině v odporujícím prostředí
Dáno: 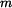 , ,  , , 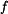 , , 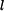 , ,
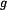 , , 
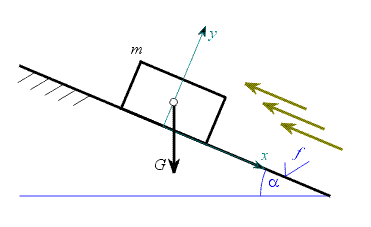
Je dán bod o hmotnosti m na drsné rovině skloněné pod úhlem Určit: 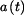 , , 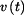 , , 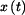
Určete průběh zrychlení, rychlosti a polohy bodu v závislosti na času. Řešení:
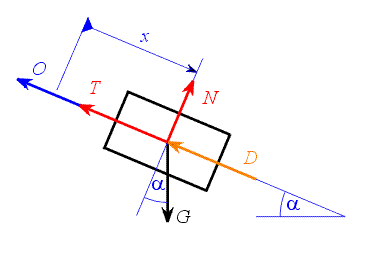
Hmotný bod v obecné poloze uvolníme (viz. Obr. 2) a k vyjádření setrvačných účinků použijeme D`Alembertův způsob. Ve vektorovém vyjádření platí:
Složkové rovnice psané ve směru os
kde je třecí síla:
odporová síla prostředí:
tíhová síla:
D`Alembertova doplňková dynamická síla:
Z rovnice (2) ještě vyjádříme sílu normálovou
Rovnici (1) vydělíme hmotností
Hlavní pohybová rovnice (3) je tedy lineární, 2. řádu, s konstantními koeficienty a nenulovou pravou stranou.
Jejím řešením je závislost 1) Homogení řešení rovnice (3) Rovnici (3) přepíšeme do homogeního tvaru:
Charakteristický polynom je:
jehož kořeny jsou:
Homogení řešení napíšeme ve tvaru:
2) Partikulární řešení Pravá strana rovnice (3) je konstanta, tedy polynom nultého skupně. Partikulární řešení odhadneme ve tvaru polynomu 1. stupně. Provedeme potřebné derivace a dosadíme do (3) .
Po dosazení:
Partikulární řešení tedy je:
3) Obecné řešení Obecné řešení je součtem řešení homogeního a partikulárního:
4) Nalezení integračních konstant Tyto konstanty určíme z počátečních podmínek uvažovaného děje. Ty jsou:
a) poloha v nulovém čase je taktéž nulová
b) rychlost v nulovém čase je nulová: Pro uplatnění počáteční podmínky b) potřebujeme rovnici popisují rychlost bodu. Zderivujeme tedy (4) podle času a dostaneme rovnici (5)
a)
b)
a) 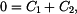
b)
Z rovnice b) plyne:
a z rovnice a) plyne:
Integrační konstanty dosadíme do (4):
tedy:
Popis rychlosti bodu získáme z rovnice (5):
Zrychlení jako derivace rychlosti je:
|
|
|
|
 .
.
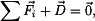
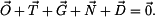
 a
a 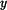 jsou:
jsou:
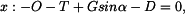
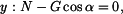
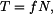
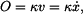
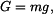
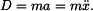
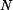 a dosadíme do (1):
a dosadíme do (1):
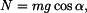
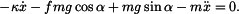
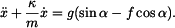
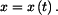
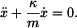
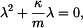
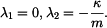
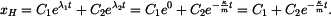
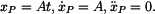
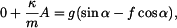
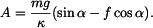

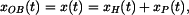
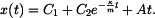
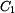 a
a 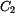
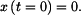
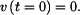 .
.