|
Navigace |
|
|
|
|
|
|
Lano stálého napětí
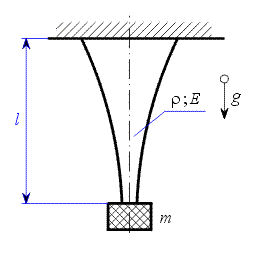
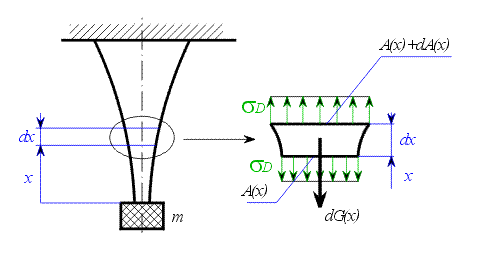
V homogenním tíhovém poli visí lano s proměnným průřezem , zatížené závažím o hmotnosti Určit : Určete funkci , která vyjadřuje velikost průřezu lana tak, aby napětí v každém místě lana bylo rovno zadané hodnotě Řešení :
Zavedeme souřadný systém například s osou Dvěma myšlenými řezy na souřadnicích Na horní i dolní plochu elementu působí předepsané napětí Rovnice rovnováhy pak má tvar
Podívejme se na objem Rovnice rovnováhy potom vypadá takto :
Po roznásobení dostaneme
čili
Integrujme obě strany rovnice
čili
kde Hodnotu
čili
a
Výsledek: Hledaná funkce je tedy
Napětí je v celé délce lana konstantní - Poměrná deformace je
a prodloužení lana je
|
|
|
|
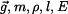
 .
.
 .
Určete prodloužení lana.
.
Určete prodloužení lana.
 o počátku na dolním konci lana a mířící nahoru.
o počátku na dolním konci lana a mířící nahoru.
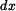 vymezíme infinetisimálně malý element lana.
vymezíme infinetisimálně malý element lana.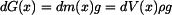 ,
kde
,
kde 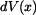 je jeho objem.
je jeho objem.
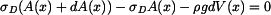 .
.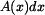 a na část , která tento válec obklopuje.
a na část , která tento válec obklopuje. 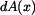 i
i 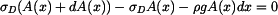 .
.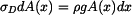 ,
,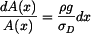 .
. ,
,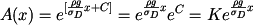 ,
,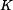 je integrační konstanta.
je integrační konstanta.
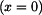 musí být napětí rovno
musí být napětí rovno 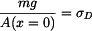 ,
,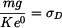
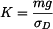 .
.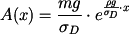 .
.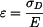
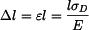 .
.