|
Navigace |
|
|
|
|
|
|
Rotující rameno
Určete : dovolené otáčky 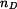 pomocí pomocí 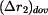 a a 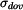 . .
Řešení : Zavedeme souřadnici
Odstředivá síla
Pro hmotnost platí
těžiště je uprostřed, tedy
Po dosazení (2) (3) a (4) do (1) dostaneme vnitřní sílu
neboli po úpravě
Napětí
a poměrnou deformaci pomocí Hookeova zákona
Všechny odvozené vztahy platí po celé délce ramene, tedy pro
jednoduchým rozborem zjistíme, že napětí nabývá na uvedeném intervalu maxima pro
čili
Po úpravě tak dostáváme
neboli
Dovolené otáčky jsou
Po dosazení
Prodloužení ramene
čili
Po integraci máme
Podle zadání musí platit
tedy
a
|
|
|
|
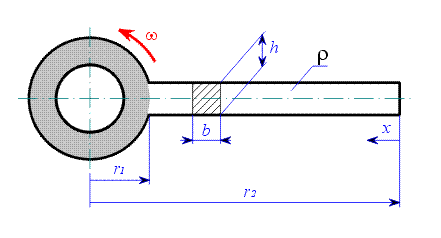
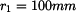
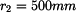
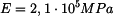
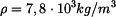
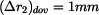
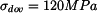
 od konce ramene. Nejprve stanovíme velikost vnitřní síly v závislosti na
od konce ramene. Nejprve stanovíme velikost vnitřní síly v závislosti na 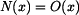
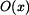 je rovna součinu hmotnosti
je rovna součinu hmotnosti  , poloměru na kterém rotuje těžiště ramene
, poloměru na kterém rotuje těžiště ramene 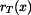 a druhé mocniny úhlové rychlosti
a druhé mocniny úhlové rychlosti
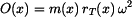 .
. ,
,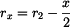 .
.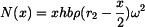 ,
,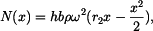
 získáme jako podíl vnitřní síly a průřezu
získáme jako podíl vnitřní síly a průřezu
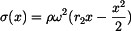
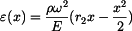 .
.
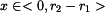 .
.
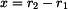 .
.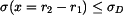 ,
,
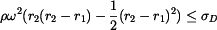 .
.
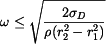 ,
,
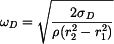 .
.
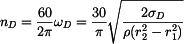 .
.
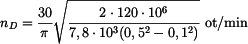
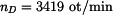 .
.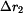 je rovno
je rovno
 ,
,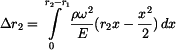 .
.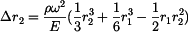 .
.
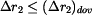 ,
,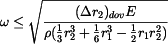
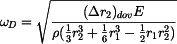 ,
,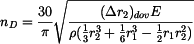 .
.
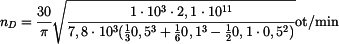
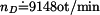 .
.