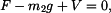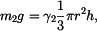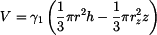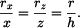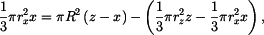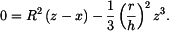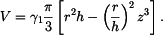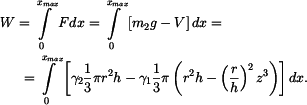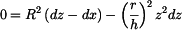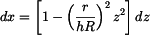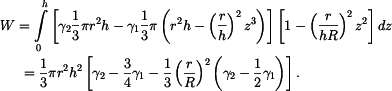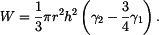|
Navigace |
|
|
|
|
|
|
Vynoření rotačního kužele
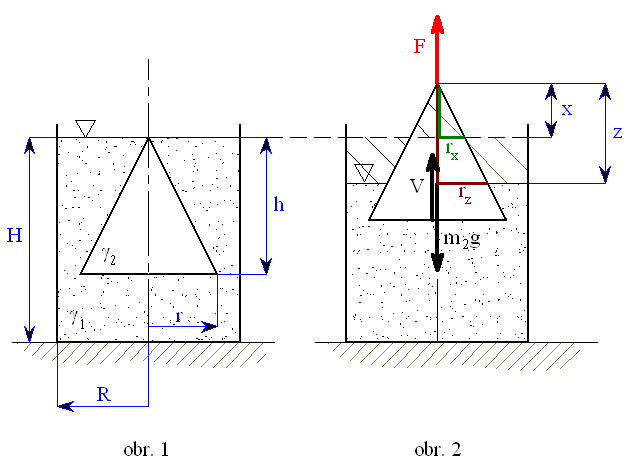
Rotační kužel výšky 
Řešení: V obecné poloze kužele platí rovnice rovnováhy
kde
je tíhová síla kužele,
je síla vztlaková, míra z je vzdálenost špičky kužele od nové hladiny, 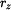 poloměr řezu kužele v této vzdálenosti. poloměr řezu kužele v této vzdálenosti.
Z podobnosti trojúhelníků (obr. 2) platí
Při vynořování kužele klesá hladina kapaliny v nádobě - vynořená špička kužele o výšce  vzhledem k původní výšce vzhledem k původní výšce  uvolnila objem v nádobě (rovnost vyšrafovaných objemů); platí uvolnila objem v nádobě (rovnost vyšrafovaných objemů); platí
odtud vyjde po úpravě
do toho vztahu dosadíme 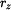 z rovnice z rovnice 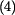
Vrátíme se k vztlakové síle 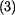 , kde po dosazení , kde po dosazení 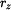 bude bude
Hledaná mechanická práce je
Nyní zderivujeme rovnici 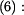
a odtud
a tento výraz dosadíme do 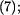
Došlo ke změně horní meze integrálu, protože jsme integrovali podle z. Poznámka: Pro případ konstantní výšky 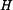 , t.j. , t.j. 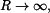 (jezero, moře), vyjde (jezero, moře), vyjde
Zpracoval: Radek Zbončák |
|
|
|
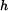 , poloměru podstavy
, poloměru podstavy  je ponořen ve válcové nádobě (poloměr podstavy
je ponořen ve válcové nádobě (poloměr podstavy  ), jeho špička se dotýká hladiny. Určete práci síly
), jeho špička se dotýká hladiny. Určete práci síly 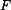 potřebnou k vynoření kužele tak, aby se jeho podstava dotýkala hladiny.
potřebnou k vynoření kužele tak, aby se jeho podstava dotýkala hladiny.