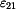|
Kulisový mechanismus
 |
 |
| Obr. 1 |
Dáno: čtyřčlenný mechanismus, 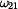 , , 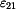
Je dán čtyřčlenný mechanismus. Hnací člen 2 je unášen úhlovou rychlostí 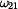 a úhlovým zrychlením a úhlovým zrychlením 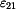 . .
Určit: 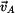 , , 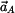 , ,  , , 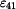
Určete rychlost a zrychlení bodu A (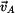 , , 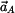 ) a úhlovou rychlost a zrychlení členu 4 ( ) a úhlovou rychlost a zrychlení členu 4 ( , , 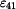 ). ).
Řešení:
 |
 |
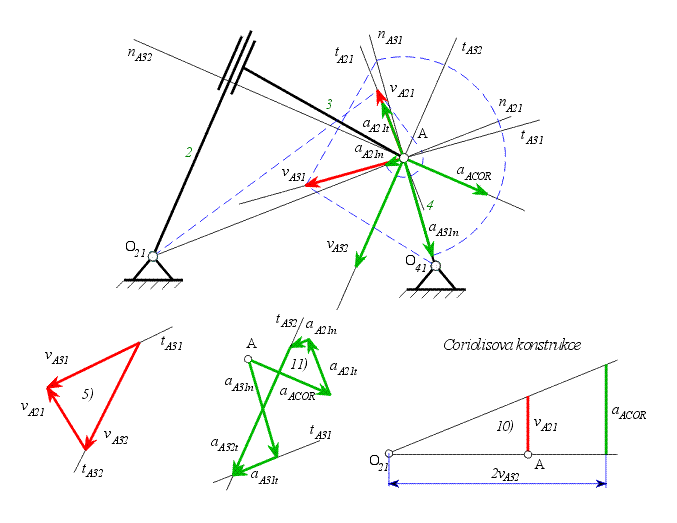
| Obr. 2 |
Řešení rychlostí:
-
při řešení použijeme rozkladu pohybu v bodě A:
-
pro rychlosti v bodě A dostaneme:
-
nositelkami rychlostí jsou příslušné tečny:
|
1) |
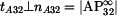 |
Tečna trajektorie bodu A v pohybu 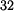 je kolmice
na normálu trajektorie bodu A v pohybu je kolmice
na normálu trajektorie bodu A v pohybu 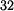 , kde normála je spojnicí bodu A a pólu pohybu , kde normála je spojnicí bodu A a pólu pohybu 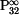 . .
|
|
2) |
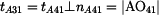
|
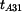 je nositelka rychlosti je nositelka rychlosti  . Je kolmá na normálu trajektorie bodu A v pohybu . Je kolmá na normálu trajektorie bodu A v pohybu 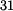 . Protože bod A náleží též členu 4, je normála . Protože bod A náleží též členu 4, je normála 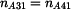 a je dána spojnicí bodu A a pólu a je dána spojnicí bodu A a pólu 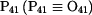 . .
|
|
3) |
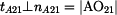
|
Nositelkou rychlosti 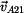 je tečna je tečna 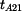 , která je kolmá na normálu
unášivého pohybu , která je kolmá na normálu
unášivého pohybu 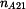 . To je spojnice bodu A a pólu pohybu . To je spojnice bodu A a pólu pohybu
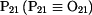 . .
|
|
4) |
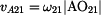
|
Velikost rychlosti unášivého pohybu 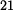 v
bodě A je dána součinem úhlové rychlosti v
bodě A je dána součinem úhlové rychlosti 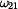 a průvodiče bodu A, tzn. vzdálenosti
a průvodiče bodu A, tzn. vzdálenosti 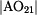 . .
|
|
5) |
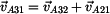
|
Sestrojíme vektorový obrazec, z kterého určíme
směry vektorů rychlostí. |
Řešení zrychlení
|
6) |
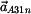
|
Normálovou složku zrychlení výsledného pohybu bodu A sestrojíme Euklidovou konstrukcí. Střed křivosti trajektorie bodu A při pohybu  , , 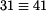 je v je v 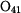
|
|
7) |
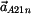
|
Použijeme Euklidovu konstrukci z rychlosti
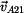 a středu křivosti a středu křivosti
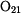 |
|
8) |
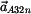
|
Protože pohyb tělesa 3 ku 2 je posuvný, bude normálová složka zrychlení 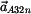 rovna rovna 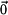 (střed křivosti trajektorie je v nekonečnu ). (střed křivosti trajektorie je v nekonečnu ). |
|
9) |
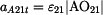
|
Tečnou složku unášivého zrychlení určíme
výpočtem. |
|
10) |
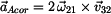
|
Velikost Coriolisova zrychlení bodu A určíme
Coriolisovou konstrukcí a směr dle pravidla pravé ruky. |
|
11) |
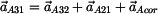
|
Nositelka tečné složky zrychlení 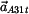 je
je 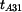 a nositelka tečné složky zrychlení a nositelka tečné složky zrychlení 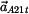 je
je 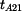 . Sestrojíme vektorový obrazec. . Sestrojíme vektorový obrazec. |
|
12) |
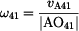
|
Velikost úhlové rychlosti 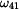 vypočteme
z velikosti rychlosti vypočteme
z velikosti rychlosti  a velikosti průvodiče bodu A
při rotaci kolem a velikosti průvodiče bodu A
při rotaci kolem 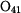
|
|
13) |
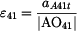
|
Velikost úhlového zrychlení 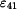 vypočteme z velikosti tečné složky zrychlení
vypočteme z velikosti tečné složky zrychlení 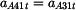 a velikosti průvodiče bodu A při rotaci kolem a velikosti průvodiče bodu A při rotaci kolem 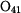 |
|
|
|
|
|
|
|
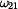 ,
,