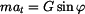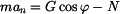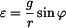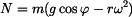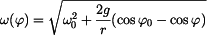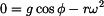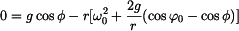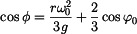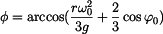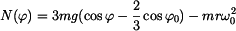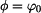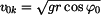|
Navigace |
|
|
|
|
|
|
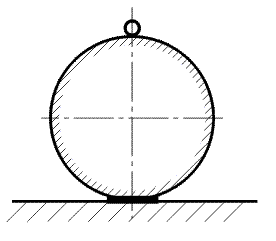
Pohyb hmotného bodu po válcové ploše
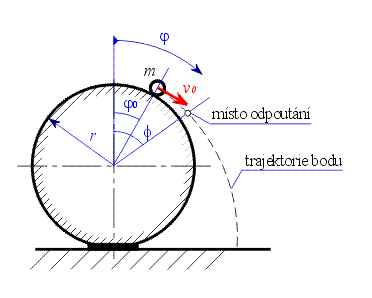
Dáno : 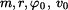 Je dán bod o hmotnosti 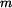 na ploše válcového tvaru,jejíž poloměr křivosti je na ploše válcového tvaru,jejíž poloměr křivosti je  .
Bod se začne pohybovat z daných počátečních podmínek polohy .
Bod se začne pohybovat z daných počátečních podmínek polohy 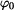 a rychlosti a rychlosti 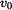 bezodporově. bezodporově.Určit :  Zjistěte úhel 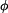 ,při kterém dojde k odpoutání hmotného bodu od válcové plochy. Určete průběh normálné síly od počátku pohybu do okamžiku
odpoutání v závislosti na úhlu ,při kterém dojde k odpoutání hmotného bodu od válcové plochy. Určete průběh normálné síly od počátku pohybu do okamžiku
odpoutání v závislosti na úhlu 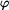 . Tedy . Tedy 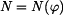 , , 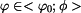 . .
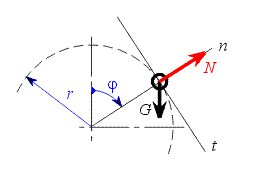
Uvolníme hmotný bod v obecné poloze a sestavíme pohybové rovnice Newtonovým způsobem v souřadném systému tečna , normála.
kde 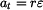 je tečné zrychlení bodu, je tečné zrychlení bodu,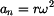 je normálné zrychlení bodu, je normálné zrychlení bodu,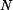 je normálová síla, je normálová síla,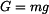 je tíhová síla. je tíhová síla.Po dosazení získáváme :
Máme-li v prvním případě řešit odtrh hmotného bodu od plochy , tedy velikost úhlu 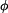 , je v tomto okamžiku styk mezi bodem a podložkou
přerušen , tedy normálová síla je nulová a rovnice (2) přejde v (4). Integrací v mezích daných počátečními podmínkami můžeme z (1) určit průběh úhlové
rychlosti. , je v tomto okamžiku styk mezi bodem a podložkou
přerušen , tedy normálová síla je nulová a rovnice (2) přejde v (4). Integrací v mezích daných počátečními podmínkami můžeme z (1) určit průběh úhlové
rychlosti.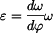 ; ; 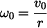 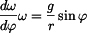 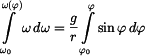 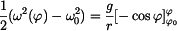
Vztah (3) dosadíme do (4) , kde je zkrácena hmotnost 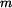 a úhel a úhel 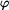 nabývá mezní hodnoty nabývá mezní hodnoty 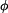 . .
odtud jednoduše vyjádříme
a tedy úhel odpoutání je
Při určování průběhu normálné síly 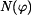 použijeme rovnici (2) , do níž dosadíme (3). použijeme rovnici (2) , do níž dosadíme (3).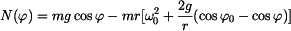 Roznásobením závorky a rutinní úpravou dostaneme
Diskuze počátečních podmínek : 1) Budou-li počáteční podmínky nulové ,
tzn. 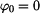 a a 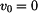 , bude bod spočívat na nejvyšším místě válcové plochy v nestabilním
rovnovážném stavu ( obr.3 ). Jakýkoli malý impuls ho uvede do pohybu. Předpokládejme tedy počáteční podmínky , bude bod spočívat na nejvyšším místě válcové plochy v nestabilním
rovnovážném stavu ( obr.3 ). Jakýkoli malý impuls ho uvede do pohybu. Předpokládejme tedy počáteční podmínky 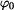 , , 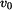 sice nenulové ale blížící se nule. Potom vztahy (7) a (8) přejdou v (9) a (10).
sice nenulové ale blížící se nule. Potom vztahy (7) a (8) přejdou v (9) a (10).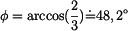 (9) (9)
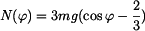 (10) (10)
Je zřejmé , že za předpokladu nekonečně malých počátečních podmínek úhel odpoutání 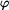 nezávisí na žádných parametrech ,
tzn. na hmotnosti bodu , poloměru válcové plochy , dokonce ani na hodnotě tíhového zrychlení. A tak kdybychom byli schopni za uvedené podmínky
experiment provést , dopadl by stejně na Zemi jako třeba na Měsíci. Bod by se odpoutal vždy pod stejným úhlem , jehož kosinus je roven nezávisí na žádných parametrech ,
tzn. na hmotnosti bodu , poloměru válcové plochy , dokonce ani na hodnotě tíhového zrychlení. A tak kdybychom byli schopni za uvedené podmínky
experiment provést , dopadl by stejně na Zemi jako třeba na Měsíci. Bod by se odpoutal vždy pod stejným úhlem , jehož kosinus je roven  . .2) Další zajímavou úvahu můžeme učinit ,
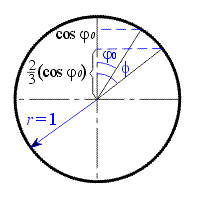
položíme-li počáteční rychlost bodu 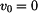 a úhel a úhel 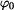 mějme libovolný z intervalu mějme libovolný z intervalu 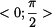 . .
Potom tedy i 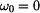 a po dosazení do (6) dostáváme , že kosinus úhlu odpoutání a po dosazení do (6) dostáváme , že kosinus úhlu odpoutání 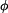 je vždy roven je vždy roven  kosinu úhlu počátečního kosinu úhlu počátečního
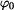 . Opět bez ohledu na parametry . Opět bez ohledu na parametry 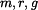 . . (11) (11)
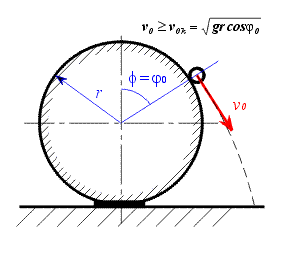
Graficky je tento vztah vyjádřen pro poloměr válcové plochy 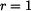 na obr.4 . na obr.4 .3) Nyní položme hmotný bod do libovolné počáteční polohy 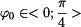 . Při nulové počáteční rychlosti . Při nulové počáteční rychlosti 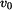 se bod na ploše udrží nejdéle. Pokud
bude se bod na ploše udrží nejdéle. Pokud
bude 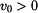 bod se od plochy odpoutá dříve. V mezním případě , bude-li rychlost bod se od plochy odpoutá dříve. V mezním případě , bude-li rychlost 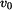 dostatečně veliká , dojde k odpoutání již v počátečním úhlu ,
viz (11). Dochází vlastně k šikmému vrhu ( obr.5 ). dostatečně veliká , dojde k odpoutání již v počátečním úhlu ,
viz (11). Dochází vlastně k šikmému vrhu ( obr.5 ).
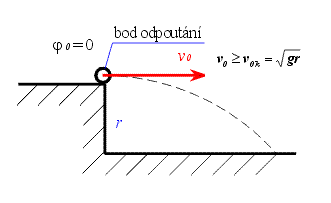
Stanovme si tuto mezní kritickou rychlost 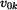 . Vztah (12) dosadíme do (6). . Vztah (12) dosadíme do (6).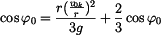 a odtud plyne
za předpokladu , že v tomto případě bude počáteční poloha bodu na vrcholu plochy  přechází vlastně situace ve vodorovný vrh
z výšky přechází vlastně situace ve vodorovný vrh
z výšky  (viz obr. 6). Rychlost (viz obr. 6). Rychlost 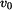 musí být větší nebo rovna musí být větší nebo rovna 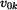 . .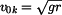 pro pro 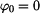
|
|
|
|