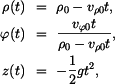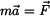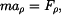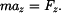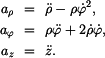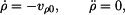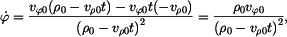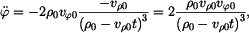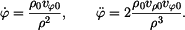|
|
DYN-02-1: I.úloha dynamiky (kinetostatika) pro volný pohyb HB
Příklad 2.1: I.úloha dynamiky (kinetostatika) pro volný pohyb hmotného bodu.
Částice plovoucí na povrchu víru má trajektorii, která je ve válcových souřadnicích popsána parametrickými rovnicemi
kde 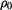 , , 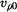 , , 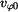 a a 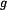 jsou dané konstanty. jsou dané konstanty.
Určete: složky 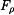 , , 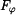 a a 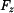 síly síly 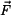 , která tento pohyb vyvolává, je-li hmotnost částice , která tento pohyb vyvolává, je-li hmotnost částice 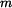 . .
Řešení:
Pohybová rovnice
má ve válcovém souřadnicovém systému složky
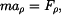 |
(1) |
 |
(2) |
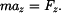 |
(3) |
Z kinematiky víme, že
V daném případě je
Protože 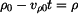 (podle zadání), můžeme také zapsat (podle zadání), můžeme také zapsat
Dosazení do (1), (2) a (3) nakonec dává
Radiální síla 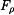 má záporné znaménko, takže působí směrem do středu víru. Je důsledkem hydrostatických sil v okolní kapalině. Transverzální složka má záporné znaménko, takže působí směrem do středu víru. Je důsledkem hydrostatických sil v okolní kapalině. Transverzální složka 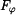 je nulová. Je to ilustrace zákona zachování momentu hybnosti, který budeme probírat později. Axiální síla je nulová. Je to ilustrace zákona zachování momentu hybnosti, který budeme probírat později. Axiální síla 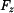 je tíhová síla částice. je tíhová síla částice.
|
|
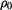 ,
, 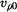 ,
, 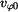 a
a 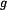 jsou dané konstanty.
jsou dané konstanty.
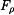 ,
, 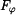 a
a 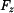 síly
síly 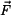 , která tento pohyb vyvolává, je-li hmotnost částice
, která tento pohyb vyvolává, je-li hmotnost částice 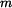 .
.
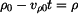 (podle zadání), můžeme také zapsat
(podle zadání), můžeme také zapsat
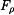 má záporné znaménko, takže působí směrem do středu víru. Je důsledkem hydrostatických sil v okolní kapalině. Transverzální složka
má záporné znaménko, takže působí směrem do středu víru. Je důsledkem hydrostatických sil v okolní kapalině. Transverzální složka 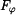 je nulová. Je to ilustrace zákona zachování momentu hybnosti, který budeme probírat později. Axiální síla
je nulová. Je to ilustrace zákona zachování momentu hybnosti, který budeme probírat později. Axiální síla 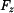 je tíhová síla částice.
je tíhová síla částice.