|
Rameno zvedané pomocí hydraulického pístu
Dáno: 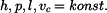
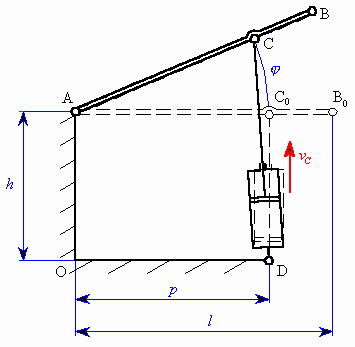
Rameno délky 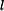 rotačně uložené v bodě A je z vodorovné polohy zvedáno hydraulickým válcem dle obrázku. Píst válce se vysunuje konstantní rychlostí rotačně uložené v bodě A je z vodorovné polohy zvedáno hydraulickým válcem dle obrázku. Píst válce se vysunuje konstantní rychlostí 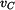 . .
 |
 |
| Obr. 1. Zadání |
Určit: 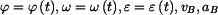
Vyšetřete závislost úhlu 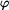 na čase, úhlové rychlosti na čase, úhlového zrychlení na čase a rychlost a zrychlení bodu B. na čase, úhlové rychlosti na čase, úhlového zrychlení na čase a rychlost a zrychlení bodu B.
Řešení:
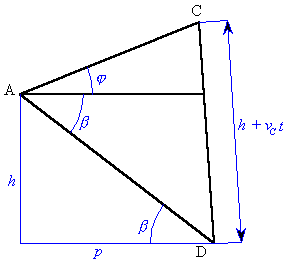
Při řešení vyjdeme z geometrie 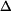 ACD (obr. 2). V něm známe vzdálenost ACD (obr. 2). V něm známe vzdálenost 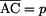 , ,  a strana a strana 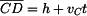 , tj. původní vzdálenost , tj. původní vzdálenost 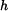 zvětšená o délku vysunutí pístu
při konstantní rychlosti zvětšená o délku vysunutí pístu
při konstantní rychlosti 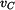 . .
 |
 |
| Obr. 2. Rozbor geometrie |
Využitím kosinové věty pro obecný 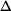 ACD dostaneme: ACD dostaneme:
 , , |
(1) |
kde  je vyjádřen vztahem je vyjádřen vztahem
 . . |
Z rovnice (1) vyjádříme úhel  závislý na čase závislý na čase 
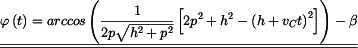 . . |
(2) |
Pro úhlovou rychlost  a úhlové zrychlení ramene a úhlové zrychlení ramene  platí: platí: 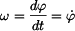 a a 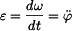 . .
Pro zjednodušení provedeme implicitní derivace rovnice (1)
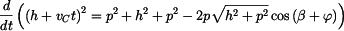 . . |
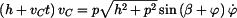 |
(3) |
Z rovnice (3) vyjádříme 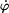
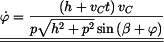 . . |
(4) |
Pro určení  zderivujeme rovnici (3) zderivujeme rovnici (3)
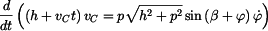 , , |
 . . |
(5) |
Z rovnice (5) vyjádříme 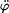
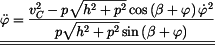 . . |
(6) |
Rychlost a zrychlení bodu B jsou dány vztahy pro pohyb bodu po kružnici:
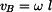 , , |
(7) |
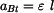 , , |
(8) |
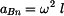 . . |
(9) |
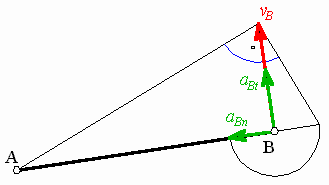
Směry vektorů rychlosti a zrychlení jsou zřejmé z obrázku 3.
 |
 |
| Obr. 3. Směry kinematických veličin |
Zpracoval: Oldřich Hybner
|
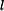 rotačně uložené v bodě A je z vodorovné polohy zvedáno hydraulickým válcem dle obrázku. Píst válce se vysunuje konstantní rychlostí
rotačně uložené v bodě A je z vodorovné polohy zvedáno hydraulickým válcem dle obrázku. Píst válce se vysunuje konstantní rychlostí 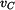 .
.
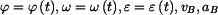
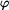 na čase, úhlové rychlosti na čase, úhlového zrychlení na čase a rychlost a zrychlení bodu B.
na čase, úhlové rychlosti na čase, úhlového zrychlení na čase a rychlost a zrychlení bodu B.
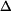 ACD (obr. 2). V něm známe vzdálenost
ACD (obr. 2). V něm známe vzdálenost 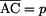 ,
,  a strana
a strana 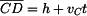 , tj. původní vzdálenost
, tj. původní vzdálenost 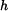 zvětšená o délku vysunutí pístu
při konstantní rychlosti
zvětšená o délku vysunutí pístu
při konstantní rychlosti 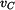 .
.
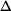 ACD dostaneme:
ACD dostaneme:
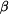 je vyjádřen vztahem
je vyjádřen vztahem
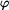 závislý na čase
závislý na čase 
 a úhlové zrychlení ramene
a úhlové zrychlení ramene  platí:
platí: 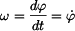 a
a 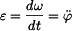 .
.
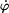
 zderivujeme rovnici (3)
zderivujeme rovnici (3)
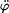


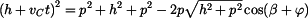 ,
, .
.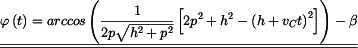 .
.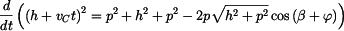 .
.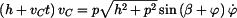
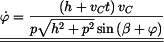 .
.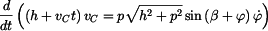 ,
, .
.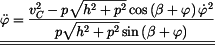 .
.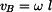 ,
,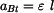 ,
,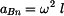 .
.