|
Navigace |
|
|
|
|
|
|
Dvakrát osazený kroucený hřídel I
Dáno: Hřídel je uložen a zatížen podle obr 1.
Určit: reakce, Řešení:
Zavedeme reakce např. tak, jako na obr.2 a zapíšeme rovnici rovnováhy:
neboli
Úloha je jednou staticky neurčitá. Vzhledem k uložení obou konců můžeme napsat deformační podmínku:
Metodou řezu nyní stanovíme velikost vnitřního krouticího momentu v úsecích I - IV , jak jsou vyznačeny na obr.2:
Polární kvadratické momenty v jednotlivých úsecích hřídele mají hodnoty:
Vzájemné natočení
čili:
Po dosazení a integraci dostáváme:
a po úpravě:
Dosazením posledního vztahu do deformační rovnice
Z rovnice rovnováhy pak:
Pro stanovení napětí nejprve určíme velikost průřezových modulů v krutu
Smyková napětí pak mají hodnoty:
Pro napětí tedy platí následující relace:
Největší smykové napětí nabývá hodnoty:
|
|
|
|

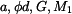

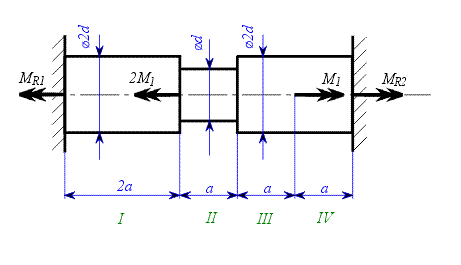
 ,
,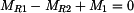 .
.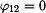 .
.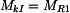 ,
,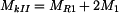 ,
,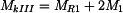 ,
,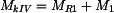 .
.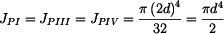 ,
,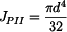 .
.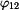 má tvar:
má tvar: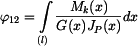 ,
,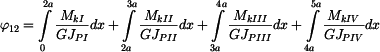 .
.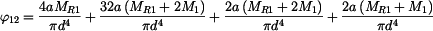 ,
,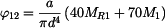 .
.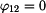 a úpravou dostáváme:
a úpravou dostáváme: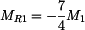 .
.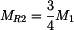 .
.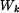 pro
jednotlivé části hřídele.
pro
jednotlivé části hřídele.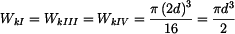 ,
,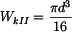 .
.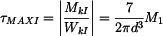 ,
,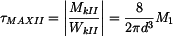 ,
,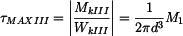 ,
,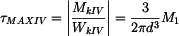 .
.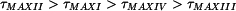 .
.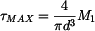 .
.