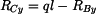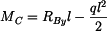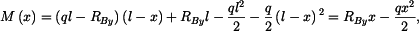|
Navigace |
|
|
|
|
|
|
Křivý prut a nosník namáhané na ohyb
Dáno: 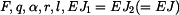
Soustava těles (křivý prut a nosník) je zatížena veličinami
Řešení:
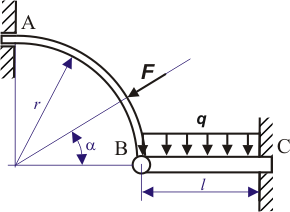
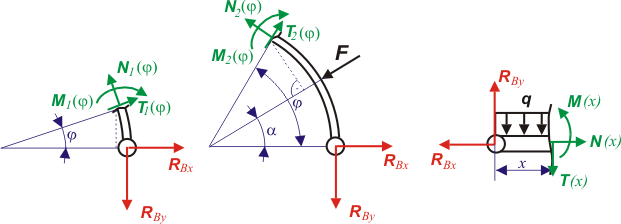
Na obr. 2 jsou zakresleny reakce v uloženích působící na jednotlivá tělesa Rovnice rovnováhy jednotlivých těles :
Neznámých reakcí je 7, rovnic rovnováhy 6. Z toho vyplývá, že soustava je jedenkrát staticky neurčitá.
Proveďme rozbor, z kterých reakcí lze vybrat staticky neurčitou do deformační podmínky. Z rovnice (1) vyplývá,
že velikost reakce
Dále určíme vnitřní statické ohybové momenty. Vliv posouvajících sil
Ohybové momenty v myšlených řezech jsou :
Energie napjatosti
Zkontrolujeme, zda energie napjatosti Nezávislé veličiny jsou: 1) vnější síly (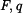 ) a reakce, které lze určit přímo z rovnic rovnováhy ( ) a reakce, které lze určit přímo z rovnic rovnováhy (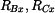 ) )
2) reakce, které jsme vybrali do deformačních podmínek ( Závislé veličiny jsou všechny ostatní reakce
( Vzhledem k tomu, že závislé veličiny se ve výrazu pro U nevyskytují, je možno formulovat
rovnici (7) :
Z rovnice (7) vypočteme Poznámka: Kdybychom zachovali rovnici (7) se staticky neurčitou reakcí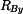 avšak výpočet momentu avšak výpočet momentu 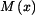 provedli např. pro druhou část tělesa BC podle obr. 4 dostaneme : provedli např. pro druhou část tělesa BC podle obr. 4 dostaneme :
Reakce
pak
což se shoduje s předchozím výrazem pro
|
|
|
|
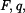
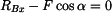
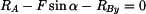
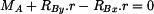
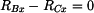
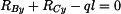
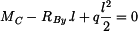
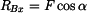 je známá. Totéž platí pro
je známá. Totéž platí pro 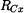 z rovnice (4). Žádná z ostatních 5 reakcí se přímo z rovnic rovnováhy nedá vypočítat, můžeme volit
kteroukoli. Např.
z rovnice (4). Žádná z ostatních 5 reakcí se přímo z rovnic rovnováhy nedá vypočítat, můžeme volit
kteroukoli. Např.
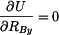
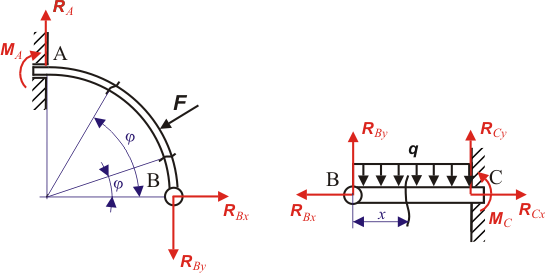
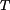 a normálových sil
a normálových sil 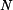 lze v řešení zanedbat. Vzhledem k volbě staticky neurčité veličiny je výhodné zvolit proměnné
lze v řešení zanedbat. Vzhledem k volbě staticky neurčité veličiny je výhodné zvolit proměnné
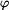 a
a  a příslušné rovnice odříznutých částí těles podle obr. 3.
a příslušné rovnice odříznutých částí těles podle obr. 3.
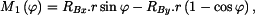
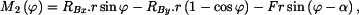
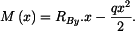
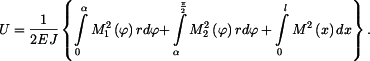
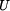 je funkcí pouze t.zv. nezávislých veličin.
je funkcí pouze t.zv. nezávislých veličin.
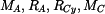 )
)
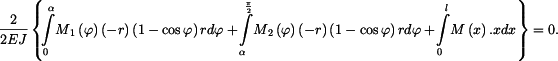
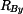 . Ostatní reakce vyplynou z rovnic (2), (3), (5) a (6).
Tato varianta řešení vede nejkratší cestou k cíli.
. Ostatní reakce vyplynou z rovnic (2), (3), (5) a (6).
Tato varianta řešení vede nejkratší cestou k cíli.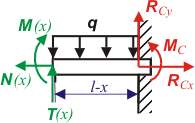
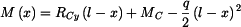
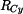 a
a 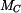 jsou závislé veličiny a je třeba je z výrazu pro
jsou závislé veličiny a je třeba je z výrazu pro