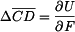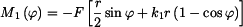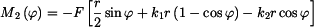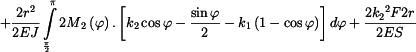|
Navigace |
|
|
|
|
|
|
Deformace tenkého křivého prutu. Vnitřní statická neurčitost.
Dáno: 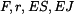
Soustava křivého prutu (A,B,C,D) o ohybové tuhosti
Určit: Určete změnu vzdálenosti míst C, D a A, B na křivém prutu po deformaci soustavy.
Řešení:
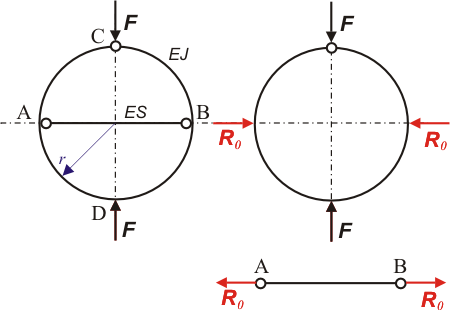
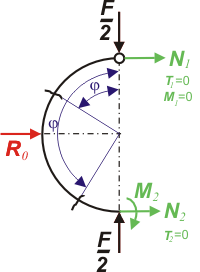
Prut AB je namáhaný podle obr.1 pouze na tah reakcí Rovnice rovnováhy odříznuté části prutu :
Třetí rovnice rovnováhy (do svislého směru) je triviální. Neznámé jsou vnitřní statické účinky
Pro výpočet energie napjatosti určíme vnitřní statické účinky (v našem případě pouze
Vyjádříme moment v intervalu pro
a v intervalu pro
Energie napjatosti celé soustavy těles je
Deformační podmínky pak jsou, derivujeme-li
Ze soustavy rovnic (3), (4) vypočteme neznámé
Vnitřní účinky
Deformaci prutu ve svislém směru (
Ohybové momenty pro výpočet energie napjatosti je třeba upravit do vztahu závislého pouze na síle
Deformace je
Po úpravě výrazu získáme skutečnou hodnotu |
|
|
|
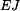 a přímého prutu (A,B) o tuhosti v tahu
a přímého prutu (A,B) o tuhosti v tahu 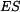 je zatížena silou
je zatížena silou 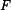
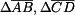
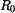 .V obecném místě křivého prutu působí vnitřní statické účinky
.V obecném místě křivého prutu působí vnitřní statické účinky 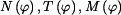 podle obr.3. Energie napjatosti a napětí způsobené normálovou silou
podle obr.3. Energie napjatosti a napětí způsobené normálovou silou 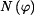 a posouvající silou
a posouvající silou 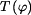 jsou nepodstatné ve srovnání s hodnotami vyvolanými ohybovým momentem
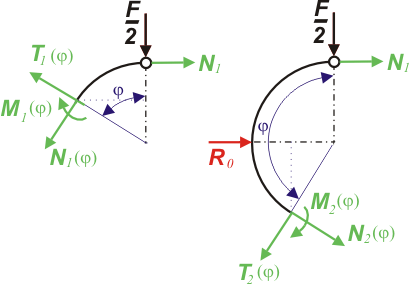
jsou nepodstatné ve srovnání s hodnotami vyvolanými ohybovým momentem  Proto je dále zanedbáme. Křivý prut má 1 osu symetrie. Na obr.2 je zakresleno výpočtové schéma poloviny prutu.
Proto je dále zanedbáme. Křivý prut má 1 osu symetrie. Na obr.2 je zakresleno výpočtové schéma poloviny prutu.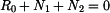
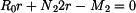
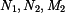 a reakce
a reakce 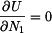
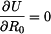
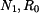 ), zde viz obr.3.
), zde viz obr.3.
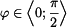


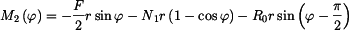
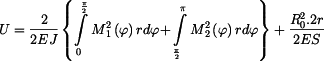
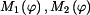 jako složené funkce :
jako složené funkce :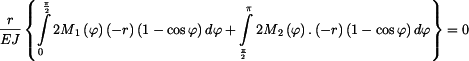
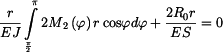
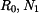
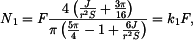
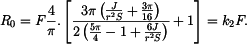
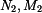 lze dopočítat z rovnic (1), (2). Deformace prutu (
lze dopočítat z rovnic (1), (2). Deformace prutu (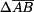 ) je stejná jako deformace přímého prutu :
) je stejná jako deformace přímého prutu :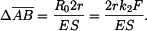
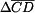 určíme z Castiglianovy věty
určíme z Castiglianovy věty