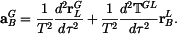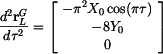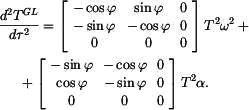|
Navigace |
|
|
|
|
|
|
KIN-07-2 Volný obecný rovinný pohyb
Dáno:
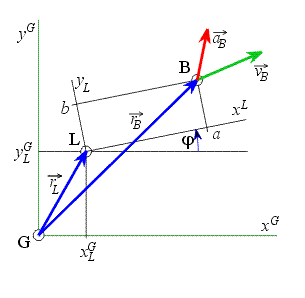
Pro polohový vektor referenčního bodu
a y-ová globální složka vektoru rychlosti jako funkce
Pro relativní rotaci okolo referenčního bodu je dáno úhlové zrychlení jako funkce
Dále josu dány konstanty
Určit:
- trajektorii
- vektor rychlosti
- vektor zrychlení
bodu o lokálních souřadnicích Řešení: Trajektorie bodu B
Pro určení trajektorie libovolného bodu musíme znát složky polohového vektoru referenčního
bodu L a polohový úhel relativní rotace, vše jako funkce nějakého parametru.
V daném případě může být parametrem hodnota
Pro y-ovou souřadnici je zadána rychlost, tj. derivace podle času. Platí
takže pro určení
Řešíme separací
a integrací s korespodujícími mezemi
Výsledek
Pro relativní rotaci je dáno Platí tedy
takže
a
Integrál na pravé straně se řeší metodou per partes. Zvolíme-li
neboli nakonec
Při použití v daných mezích tak je
Dále je
takže separací
a integrací
dostáváme
Parametrická rovnice trajektorie je pak
neboli
Vektor rychlosti bodu B v GSS dostanemme derivováním (3) podle času. Protože ale
je
V našem případě je
přičemž Vektor zrychlení bodu B v GSS dostaneme derivováním (5) podle času s přihlédnutím k (4). Pak
V daném případě je
a
Zpracoval: Pavel Čapek |
|
|
|
 je dána
je dána 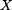 -ová globální souřadnice jako funkce
-ová globální souřadnice jako funkce
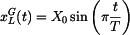
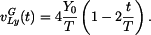
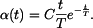
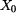 ,
, 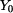 ,
, 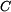 ,
,  a počáteční podmínky
a počáteční podmínky 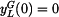 ,
,
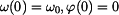 .
.
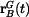
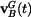
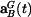
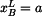 ,
, 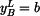 .
.
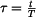 .
.
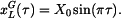
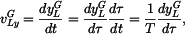
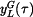 máme dif. rovnici
máme dif. rovnici
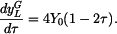
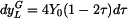
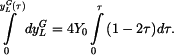
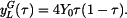
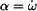 .
.
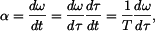
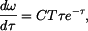
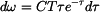

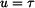 a
a 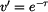 ,
bude
,
bude 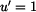 a
a 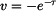 , takže
, takže
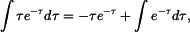
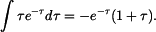
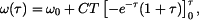
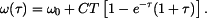
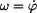 . Platí tedy
. Platí tedy
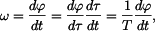
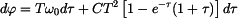
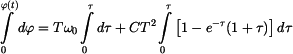
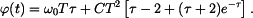
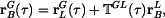
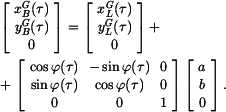
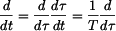
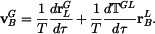
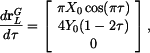
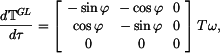
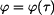 podle (2) a
podle (2) a 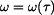 podle (1)
a
podle (1)
a