|
Navigace |
|
|
|
|
|
|
KIN-02-3 Přímočarý pohyb, nezávisle proměnná dráha
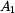 , , 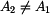 , , 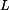 , ,
viz obr.1,
při okrajových podmínkách
Určit: Řešení: Z definice
vyplývá
Separace proměnných
Pro určení
s výsledkem
Z toho
Pro určení průběhu
výchází
Ve 2. subintervalu, kde
vychází
resp.
Podmínka spojitosti v
Pro určení času
a použijeme definiční vztah
resp.
Separace proměnných nyní bude
Integraci je možné provést v konstantních mezích, sobě navzájem odpovídajících
Výsledek integrace je
takže
Pro určení celkového času
příslušnou diferenciální rovnici separujeme do tvaru
a integrujeme v konstantních mezích
Integrál na levé straně řešíme substitucí
neboli
Rovnice (2) pak bude
Z toho
Po dosazení za
Když budeme separované diferenciální rovnice pro 1. a 2. subinterval integrovat
v proměnných mezích, můžeme určit funkci V 1. subintervalu
Ve 2. subintervalu
Funkce
Protože funkce Zpracoval: Pavel Čapek |
|
|
|
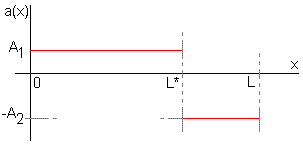
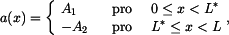
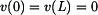 a podmínce spojitosti
a podmínce spojitosti
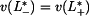 .
.
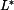 ,
, 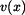 a časy
a časy 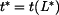 ,
,
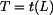 .
.
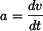
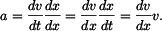
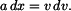
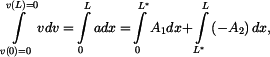
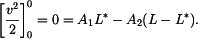
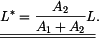

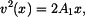
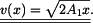
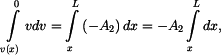
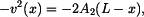
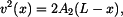

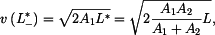
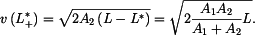
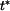 vyjádříme rychlost v 1. subintervalu jako
vyjádříme rychlost v 1. subintervalu jako

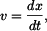
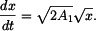
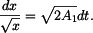
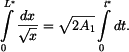
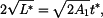
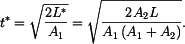
 vyjádříme rychlost ve 2. subintervalu jako
vyjádříme rychlost ve 2. subintervalu jako
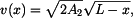
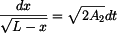
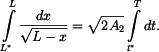
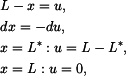
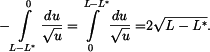
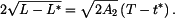
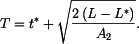
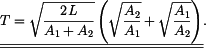
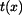 .
.
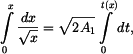
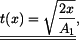
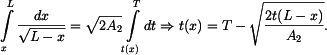
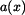 vyneseme
do grafů (obr. 2).
vyneseme
do grafů (obr. 2).
