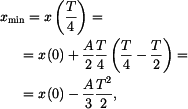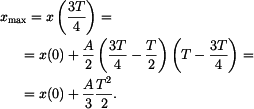|
Navigace |
|
|
|
|
|
|
KIN-02-2 Periodický pohyb přímočarý
Dáno: průběh 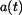 během jedné periody během jedné periody 
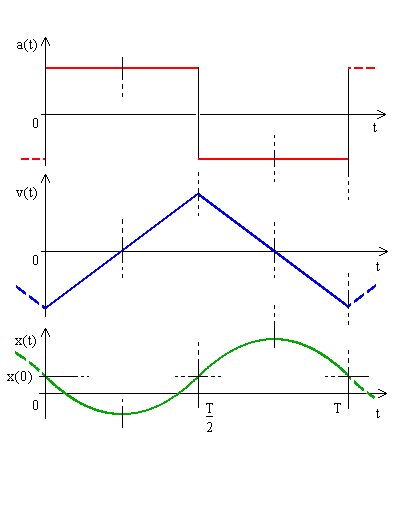
znázorněno v grafu (obr.1),
a podmínky periodicity
 a výchylka a výchylka  musí být spojité. musí být spojité.
Určit: vztah mezi Řešení: Obecně platí definice
Separace proměných a integrace
Výsledek po integraci
Analogicky pro výchylku
1. Aplikace na interval
Zde je Dosazením do rovnice (1) dostaneme
Dosazením do rovnice (2) dostaneme
což dává
Hodnoty na konci intervalu jsou
S těmito hodnotami vstupují průběhy do 2. intervalu.
2. Aplikace (1) a (2) na interval
Zde je Dosazením do rovnice (1) dostaneme
Dosazením do rovnice (2) dostaneme
což dává
Nyní dosadíme z (3) a (4) za
a
Hodnoty na konci 2. subintervalu jsou
a
Nyní aplikujeme podmínky periodicity. Podmínka pro zrychlení je splněna zadáním. Podmínka pro rychlost aplikována na (7) dává
Podmínka pro výchylku aplikována na (8) dává
Aplikace podmínek periodicity neurčuje žádnou hodnotu pro
Nakonec dosadíme za
V 2. subintervalu bude podle (5) a (6)
Hodnoty uprostřed intervalu
Výsledky ukazují, že rychlost je spojitá, po částech lineární funkce
a výchylka je spojitá, po částech kvadratická funkce
V grafickém znázornění je to "pilovitý" průběh pro rychlost a navazující paraboly pro výchylku, viz obr.2. Extrémy výchylky navstávají v časech, kdy rychlost (derivace dráhy) je nulová; minimum v 1. subintervalu, protože zde je zrychlení (2. derivace dráhy) kladné
Zpracoval: Jan Blažek |
|
|
|
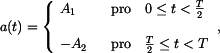
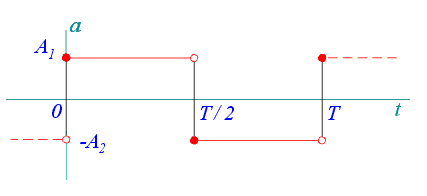
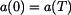 pro zrychlení
pro zrychlení
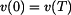 pro rychlost
pro rychlost
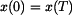 pro výchylku, dráhu,
pro výchylku, dráhu,
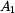 ,
,  ;
; 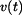 ,
, 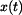
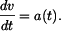
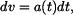
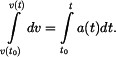
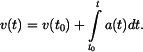
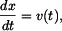
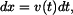
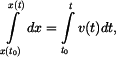
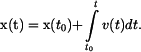
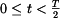
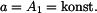 ,
, 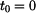 .
.
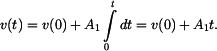
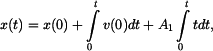
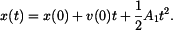
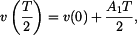
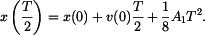
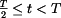
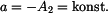 ,
, 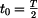 .
.
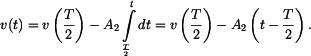
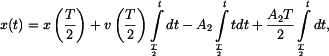
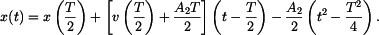
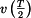 a
a 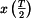 . Dostaneme
. Dostaneme
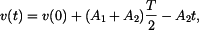
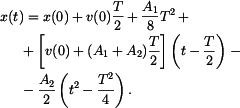
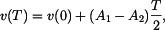
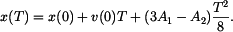
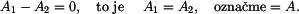
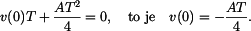
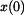 . Je tedy
. Je tedy 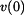 do vyšších vztahů. V prvním subintervalu tak bude
do vyšších vztahů. V prvním subintervalu tak bude
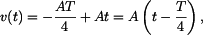
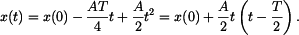
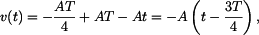
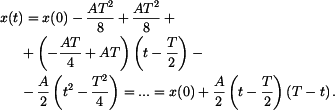
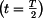 jsou podle (3) a (4)
jsou podle (3) a (4)
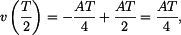
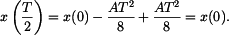
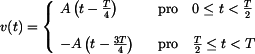
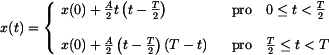
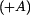 a maximum je v 2. subintervalu, protože zde je zrychlení záporné
a maximum je v 2. subintervalu, protože zde je zrychlení záporné 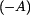 . Hodnoty extrémů jsou:
. Hodnoty extrémů jsou: