|
Cívka s lanem na nakloněné rovině
Dáno: 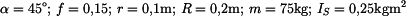
Válcová cívka se odvíjí z lana na nakloněné rovině. Počáteční rychlost
je 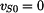 . .
 |
 |
| Obr. 1. Zadání |
Určit:
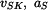
Určete jakou rychlost 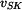 bude mít střed válce S potom, co urazí dráhu bude mít střed válce S potom, co urazí dráhu 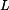 . Dále určete zrychlení . Dále určete zrychlení 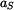 tohoto středu. tohoto středu.
Řešení:
Uvolnění válce: Na válec působí akční i reakční síly: - síla  v laně v laně
|
|
- síla 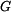 v bodě S v bodě S
|
|
|
- normálová reakce 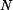
|
|
|
- třecí síla 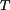
|
 |
 |
| Obr. 2. Uvolnění tělesa |
Jedná se o obecný rovinný pohyb - rotace válce kolem středu S a jeho posuv.
Zavádíme kinematické veličiny: úhlové zrychlení
 a zrychlení středu válce a zrychlení středu válce 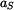 . .
Vyjdeme z pohybových rovnic
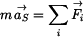 , , |
(1) |
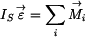 . . |
(2) |
Rozepíšeme rovnice (1), (2) do složek
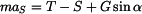 , , |
(3) |
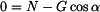 , , |
(4) |
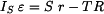 . . |
(5) |
Rovnice (3), (4), (5) doplníme vztahem pro smykové tření
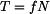 |
(6) |
a kinematickou vazbou
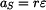 . . |
(7) |
Postupným dosazováním rovnic (3) až (7) dostaneme vlastní pohybovou rovnici tělesa
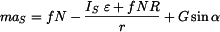 , , |
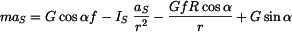 , , |
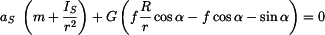 , , |
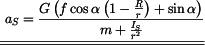 . . |
Výsledné zrychlení je konstantní.
Rychlost středu válce S na konci dráhy je dána rovnicí
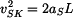 , , |
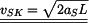 . . |
Číselné výsledky:
Zrychlení:
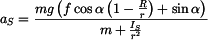
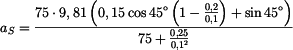
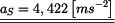
Rychlost:
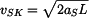
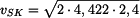

Autor: Iva Petríková, Zpracoval: Oldřich Hybner
|
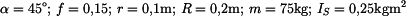
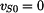 .
.
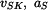
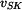 bude mít střed válce S potom, co urazí dráhu
bude mít střed válce S potom, co urazí dráhu 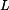 . Dále určete zrychlení
. Dále určete zrychlení 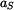 tohoto středu.
tohoto středu.
 v laně
v laně
 a zrychlení středu válce
a zrychlení středu válce 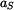 .
.
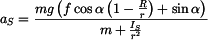
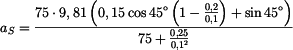
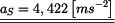
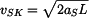
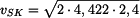



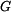 v bodě S
v bodě S

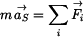 ,
,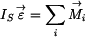 .
.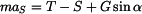 ,
,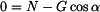 ,
,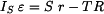 .
.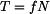
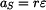 .
.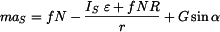 ,
,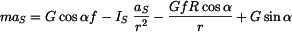 ,
,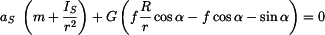 ,
,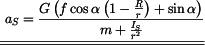 .
.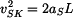 ,
,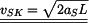 .
.