|
Navigace |
|
|
|
|
|
|
Setrvačné účinky rotujících hmot - čtvrtválec
Dáno: 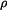 , ,  , ,  , , 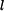 , ,  , ,  , , 
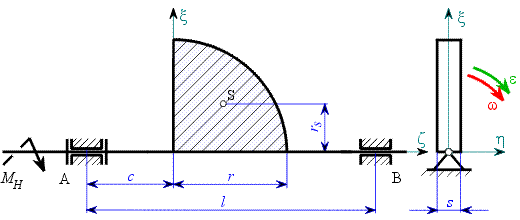
Rotující těleso má v naznačené poloze zadaný pohyb (obr.1). Je dána hustota rotujícího útvaru
Určit: Určeme reakce v ložiskách způsobené setrvačnými účinky a potřebnou hnací dvojici. Pasivní odpory zanedbejme.
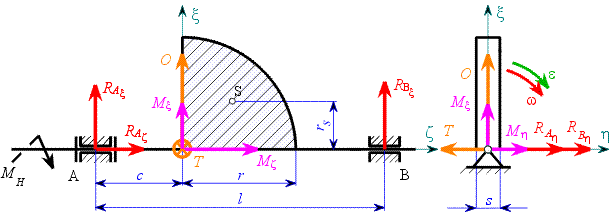
Řešení: Uvolnění:
Jde o prostorový případ tělesa rotujícího kolem stálé osy. Setrvačné účinky nahradíme redukčním párem
Odstředivou a tečnou složku D´Alembertovy síly vyjádříme jako:
Poloha těžiště (hmotného střediska) čtvrtkruhu
Složky dynamického momentu jsou vyjádřeny:
Tím, že jsme k vyjádření dynamických účinků použili D´Alembertova principu, můžeme pro rotor psát soustavu šesti rovnic rovnováhy (sílu
Osový moment setrvačnosti a deviační momenty vypočteme:
Jestliže je tloušťka Velikosti reakcí jsou:
Tím jsme získali soustavu sedmnácti rovnic pro stejný počet neznámých:
Hledané reakce v ložiskách a hnací moment vycházejí následovně:
Výsledky pro konkrétní zadané hodnoty:
|
|
|
|
 ,
,  ,
, 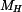
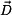 ,
, 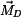 v počátku zvoleného souřadného systému
v počátku zvoleného souřadného systému
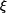 ,
, 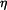 ,
,  . Dále zavedeme složky reakcí; v levém ložisku, které přenáší
také osovou sílu, to budou:
. Dále zavedeme složky reakcí; v levém ložisku, které přenáší
také osovou sílu, to budou:
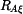 ,
, 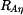 ,
, 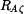 ,
v pravém
,
v pravém 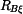 ,
, 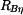 . Platí:
. Platí: 
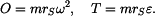
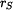 a hmotnost čtvrtválce
a hmotnost čtvrtválce 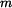 jsou:
jsou:
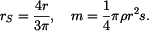

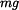 zanedbáme). První tři rovnice jsou složkové a další momentové.
zanedbáme). První tři rovnice jsou složkové a další momentové.

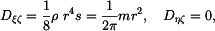
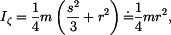
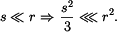
 , lze vliv tloušťky na velikost momentu
setrvačnosti zanedbat.
, lze vliv tloušťky na velikost momentu
setrvačnosti zanedbat. 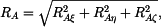
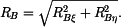
 ,
,  ,
, 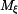 ,
, 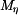 ,
, 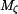 ,
, 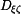 ,
, 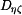 ,
, 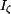 ,
, 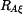 ,
, 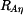 ,
, 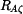 ,
, 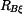 ,
, 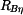 ,
, 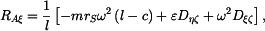
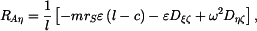
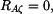
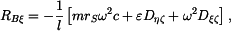
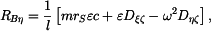
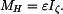
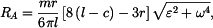
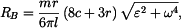
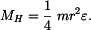
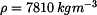 ,
,
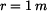 ,
,
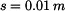 ,
,
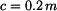 ,
,
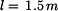 ,
,
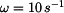 ,
,
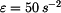 ,
,
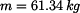 ,
,
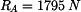 ,
,
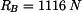 ,
,