

|
|
Fyzické kyvadlo
Dáno: 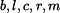 ; počáteční podmínky: ; počáteční podmínky: 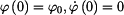
Hmotná homogenní obdélníková deska s kruhovým otvorem se kývá kolem vodorovné osy  . .
 |
 |
| Obr. 1. Zadání |
Určit: 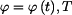
Vyšetřete pohyb tělesa a určete dobu kmitu 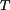 . .
Řešení:
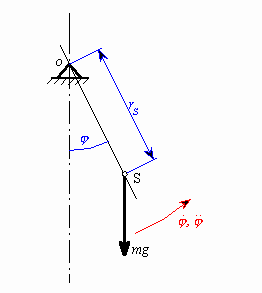
Těleso vychýlíme z rovnovážné polohy, ve směru rostoucí výchylky zvolíme kladný smysl úhlového zrychlení.
 |
 |
| Obr. 2. Rozbor |
Pohybová rovnice rotačního pohybu tělesa je
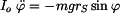 , , |
(1) |
kde 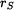 je vzdálenost těžiště od osy rotace je vzdálenost těžiště od osy rotace  . .
Pro řešení je třeba určit polohu těžiště 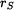 a hmotový moment setrvačnosti tělesa a hmotový moment setrvačnosti tělesa 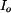 . .
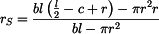 . . |
Moment setrvačnosti obdélníka k těžišti S1 je
 . . |
Moment setrvačnosti kruhu k těžišti S2 je
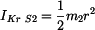 . . |
Moment setrvačnosti útvarů k ose rotace  vypočteme užitím Steinerovy věty vypočteme užitím Steinerovy věty
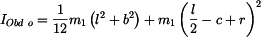 , , |
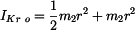 . . |
Hmotový moment setrvačnosti celého tělesa k ose rotace je
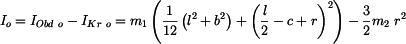 , , |
kde
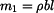 , , |
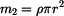 , , |
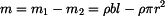 , , |
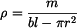 , , |
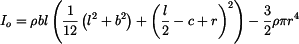 , , |
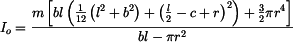 . . |
Rovnice (1) je vlastní pohybová rovnice. Jde o nelineární diferenciální rovnici 2. řádu.
Zjednodušeně ji lze řešit za předpokladu malých výchylek kolem rovnovážné polohy,
kdy platí 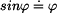 . .
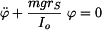 . . |
(2) |
Rovnice (2) je lineární diferenciální rovnice 2. řádu a popisuje harmonické kmitání. Řešení předpokládáme
ve tvaru
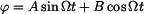 , , |
(3) |
kde
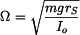 . . |
Konstanty A a B určíme z počátečních podmínek: 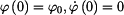
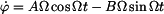 . . |
(4) |
Dosazením počátečních podmínek v čase 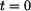 do rovnic (3), (4) dostáváme do rovnic (3), (4) dostáváme
 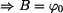 , , |
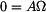 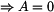 . . |
Výsledky:
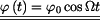
Doba kmitu:
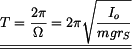
Pro případ výchylek větších než 5° rovnici (1) řešíme numericky.
Autor: Iva Petríková, Zpracoval: Oldřich Hybner
|
|
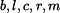 ; počáteční podmínky:
; počáteční podmínky: 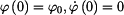
 .
.
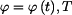
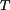 .
.
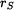 je vzdálenost těžiště od osy rotace
je vzdálenost těžiště od osy rotace  .
.
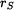 a hmotový moment setrvačnosti tělesa
a hmotový moment setrvačnosti tělesa 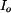 .
.
 vypočteme užitím Steinerovy věty
vypočteme užitím Steinerovy věty
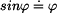 .
.
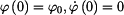
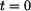 do rovnic (3), (4) dostáváme
do rovnic (3), (4) dostáváme
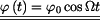
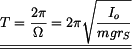


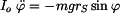 ,
,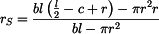 .
. .
.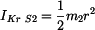 .
.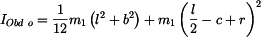 ,
,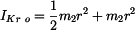 .
.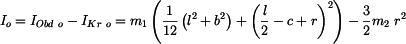 ,
,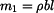 ,
,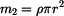 ,
,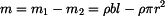 ,
,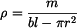 ,
,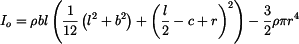 ,
,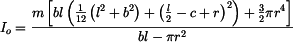 .
.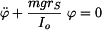 .
.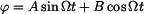 ,
,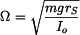 .
.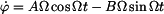 .
.
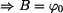 ,
,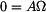
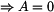 .
.