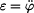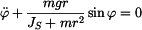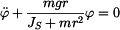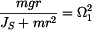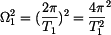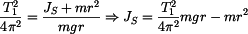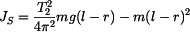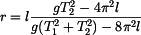|
Navigace |
|
|
|
|
|
|
Zjištění momentu setrvačnosti ojnice k ose procházející těžištěm a polohy těžiště
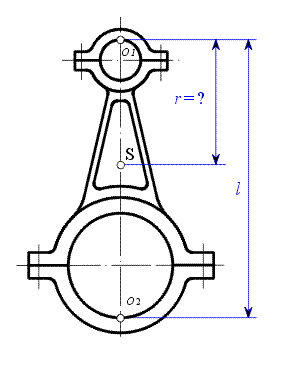
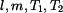 Je dána ojnice s rozměrem 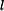 a hmotností a hmotností 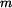 . Dvojím odkýváním ojnice kolem os . Dvojím odkýváním ojnice kolem os 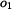 a a 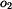 byly stanoveny
doby kmitu byly stanoveny
doby kmitu 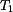 a a 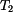 . .Určit : 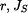 Určete vzdálenost těžiště  od osy od osy 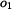 a moment setrvačnosti ojnice k ose procházející těžištěm. a moment setrvačnosti ojnice k ose procházející těžištěm.
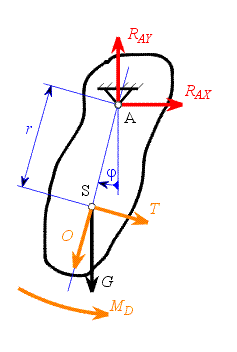
Ojnici můžeme nahradit obecným tělesem , které uvolníme D'alembertovým způsobem. Předpokládejme kyv kolem osy 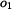 . .Polohu tělesa měříme úhlovou souřadnicí 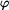 . .Rovnice rovnováhy :
kde doplňkové D'Alembertovy dynamické účinky jsou 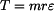 , , 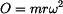 , , 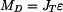 a tíhová síla je 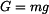 . .Pro nalezení veličin  a a 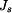 nám postačí rovnice (3). Zbylé dvě by sloužily k výpočtu reakce v místě uložení nám postačí rovnice (3). Zbylé dvě by sloužily k výpočtu reakce v místě uložení 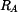 .
Tedy .
Tedy
a po úpravě do standartního tvaru dostáváme diferenciální rovnici pohybu fyzikálního kyvadla.
Rovnice (4) je nelineární. Avšak za předpokladu , že ojnici rozkýveme tak , aby souřednice 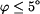 , můžeme napsat , že , můžeme napsat , že 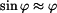 .
Potom dostáváme lineární diferenciální rovnici (5) , kde výraz u .
Potom dostáváme lineární diferenciální rovnici (5) , kde výraz u 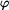 značí kvadrát vlastní frekvence kývání ojnice značí kvadrát vlastní frekvence kývání ojnice 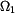 . .
Poznamenejme , že jmenovatel výrazu v (6) , 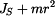 , je moment setrvačnosti kyvadla k ose , je moment setrvačnosti kyvadla k ose 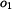 procházející bodem procházející bodem 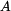 . .Dále platí :
Porovnáním rovnic (6) a (7) vyjádříme moment setrvačnosti 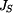 . .
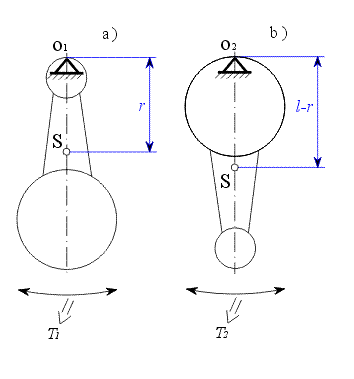
Nyní uskutečníme kyvy ojnice kolem os 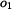 a a 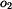 a zjistíme periody kmitů a zjistíme periody kmitů 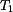 a a 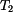 . .
Obdobou rovnice (8) pro případ měření a) na obr. 3 je rovnice (9) odpovídající provedení experimentu b) , kde vzdálenost těžiště od osy rotace 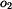 je
je 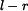 . .
Porovnáním pravých stran rovnice (8) a (9) , kde jedinou neznámou je poloha těžiště  , dostáváme : , dostáváme :
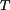 a a 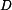 umístíme do místa rotace umístíme do místa rotace 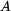 . .Všechny rovnice odvozené pro původní případ zůstávají v platnosti. Pouze za D'Alembertův dynamický doplňkový moment dosadíme 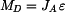 . .
|
|
|
|
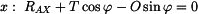
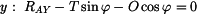
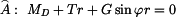
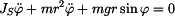 ,
, 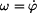 ,
,