|
KIN-02-1 Volný pád / svislý vrh
 |
 |
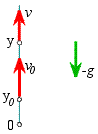
| obr. 1 |
Dáno: 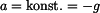 , ,
počáteční podmínky: 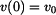 , , 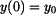 . .
Jde o přímočarý pohyb podél vertikální přímky.
Určit: závilosti 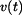 , , 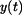 a a 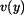 . .
Řešení:
Dané zrychlení je podle definice derivací rychlosti podle času
Separace proměnných a integrace v sobě odpovídajících mezích
Výsledek integrace
Vypočtená rychlost je dále podle definice derivací dráhy podle času
Další separace proměnných a integrace v sobě odpovídajících mezích
Výsledek integrace
Vypočtené funkce 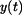 , , 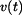 a zadanou a zadanou 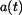 nakreslíme do grafů (obr.2). Znázorníme závislost řešení na počátečních podmínkách. nakreslíme do grafů (obr.2). Znázorníme závislost řešení na počátečních podmínkách.
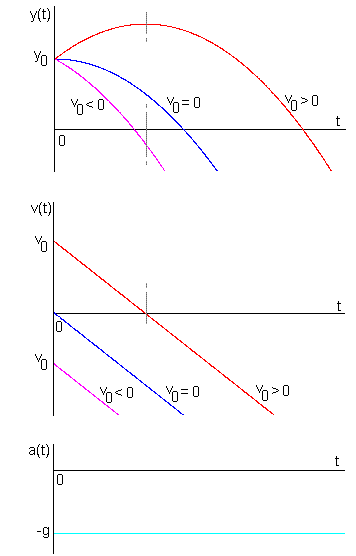 |
 |
| obr. 2 |
Pozor:
Protože se jedná o grafy funkcí a jejich derivací nebo integrálů, musejí grafy odpovídat známým vztahům mezi nimi. Zde např. lokálnímu extrému 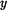 odpovídá odpovídá 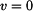 . .
Zbývá určit závislost 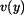 . Použijeme identitu . Použijeme identitu
Dosadíme za  , separujeme proměnné a integrujeme v sobě odpovídajících mezích. , separujeme proměnné a integrujeme v sobě odpovídajících mezích.
Výsledek integrace
resp.:
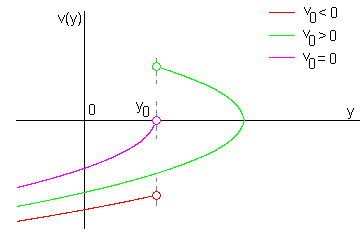
Odpovídajícím grafem je podle obr.3 parabola s osou na ose 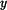 , s vrcholem v bodě, kde je , s vrcholem v bodě, kde je  , tj. , tj. 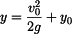 , otevřená doleva a procházející bodem , otevřená doleva a procházející bodem 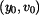 . Řešení odpovídá jen část paraboly pod hodnotou . Řešení odpovídá jen část paraboly pod hodnotou  . Jsou znázorněny paraboly pro . Jsou znázorněny paraboly pro 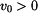 , , 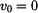 a a 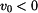 : :
 |
 |
| obr. 3 |
Zpracoval: Pavel Čapek
| 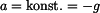 ,
,

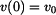 ,
, 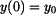 .
.
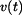 ,
, 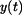 a
a 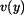 .
.
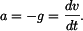
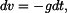
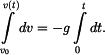

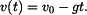
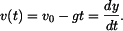
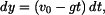
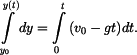
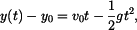
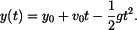
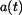 nakreslíme do grafů (obr.2). Znázorníme závislost řešení na počátečních podmínkách.
nakreslíme do grafů (obr.2). Znázorníme závislost řešení na počátečních podmínkách.
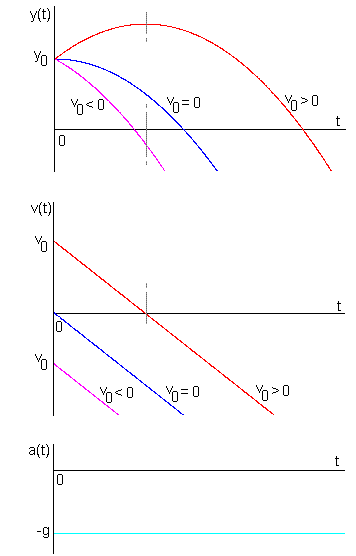
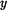 odpovídá
odpovídá 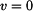 .
.
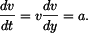
 , separujeme proměnné a integrujeme v sobě odpovídajících mezích.
, separujeme proměnné a integrujeme v sobě odpovídajících mezích.
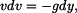
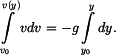
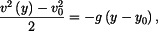
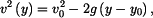
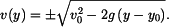
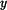 , s vrcholem v bodě, kde je
, s vrcholem v bodě, kde je  , tj.
, tj. 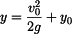 , otevřená doleva a procházející bodem
, otevřená doleva a procházející bodem 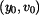 . Řešení odpovídá jen část paraboly pod hodnotou
. Řešení odpovídá jen část paraboly pod hodnotou  . Jsou znázorněny paraboly pro
. Jsou znázorněny paraboly pro 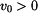 ,
, 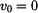 a
a 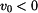 :
:
