|
Dvakrát osazená tyč v tíhovém poli
Dáno: 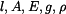
Určete: průběh napětí na tyči a změnu její délky
Řešení:
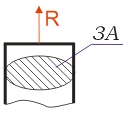 |
 |
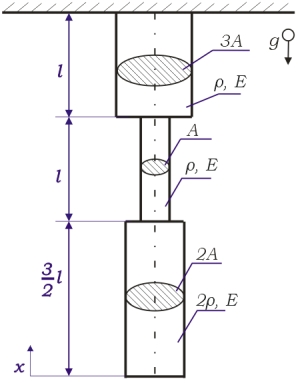
| obr. 1 |
Zavedeme reakci v uložení (viz obr.1) a napíšeme rovnici rovnováhy
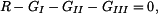
|
(1) |
kde 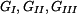 jsou tíhy horní, střední a dolní části tyče jsou tíhy horní, střední a dolní části tyče
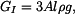
|
(2) |
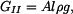
|
(3) |
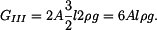
|
(4) |
Velikost reakce R bude tedy:
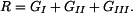 |
(5) |
Po dosazení
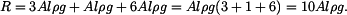 |
(6) |
Metodou řezu zdola stanovíme vnitřní sílu ve spodní části tyče 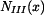
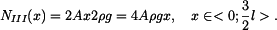
|
(7) |
Vnitřní síla 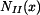 ve střední části tyče je dána tíhou celé spodní části tyče a tíhou fragmentu střední části, která se nachází pod myšleným řezem. ve střední části tyče je dána tíhou celé spodní části tyče a tíhou fragmentu střední části, která se nachází pod myšleným řezem.
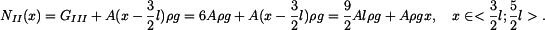 |
(8) |
Vnitřní síla 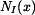 v horní části tyče je dána tíhou spodní a střední části tyče a tíhou fragmentu horní části, která se nachází pod myšleným řezem. v horní části tyče je dána tíhou spodní a střední části tyče a tíhou fragmentu horní části, která se nachází pod myšleným řezem.
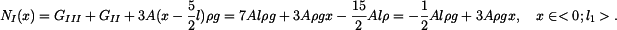 |
(9) |
Napětí ve spodní, střední a horní části
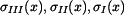 má tvar: má tvar:
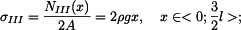
|
(10) |
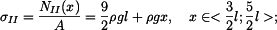
|
(11) |
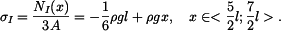
|
(12) |
Poměrné deformace 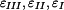 dostaneme z Hookova zákona
dostaneme z Hookova zákona
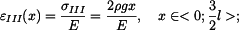 |
(13) |
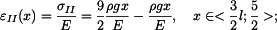 |
(14) |
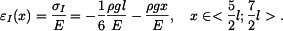 |
(15) |
Změnu délky  získáme integrací poměrné deformace získáme integrací poměrné deformace
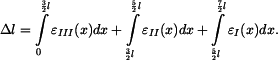 |
(16) |
po dosazení, integraci a úpravě dostaneme:

|
(17) |
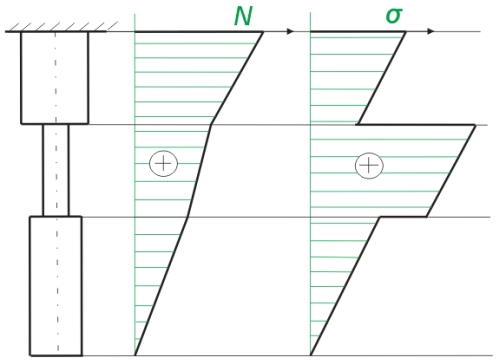
Obr.2: průběh vnitřní síly 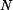 a napětí a napětí 
Zpracoval: Ondra a Jiřa
| 
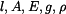
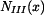
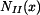 ve střední části tyče je dána tíhou celé spodní části tyče a tíhou fragmentu střední části, která se nachází pod myšleným řezem.
ve střední části tyče je dána tíhou celé spodní části tyče a tíhou fragmentu střední části, která se nachází pod myšleným řezem.


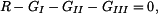
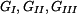 jsou tíhy horní, střední a dolní části tyče
jsou tíhy horní, střední a dolní části tyče
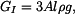
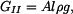
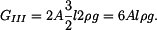
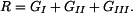
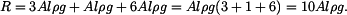
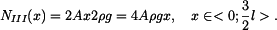
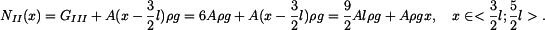
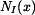 v horní části tyče je dána tíhou spodní a střední části tyče a tíhou fragmentu horní části, která se nachází pod myšleným řezem.
v horní části tyče je dána tíhou spodní a střední části tyče a tíhou fragmentu horní části, která se nachází pod myšleným řezem.
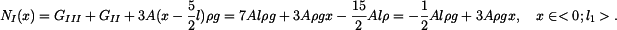
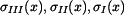 má tvar:
má tvar: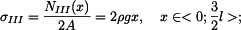
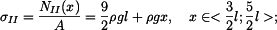
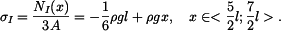
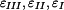 dostaneme z Hookova zákona
dostaneme z Hookova zákona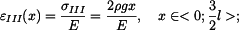
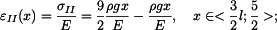
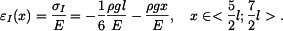
 získáme integrací poměrné deformace
získáme integrací poměrné deformace
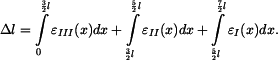

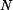 a napětí
a napětí 