|
Navigace |
|
|
|
|
|
|
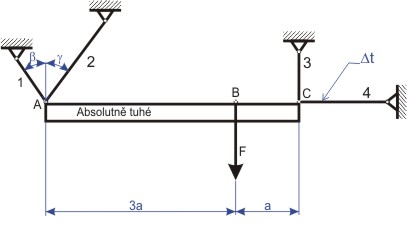
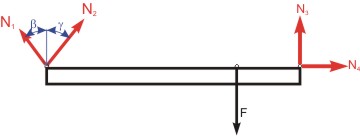
Trám na čtyřech prutech
Určete : Síly v prutech Řešení: Trám uvolníme, zakreslíme všechny síly, které na něj půsubí a zapíšeme rovnice rovnováhy.
Úloha je jednou staticky neurčitá
Zakreslíme trám v obecné poloze po deformaci a vyjádříme změny délek jednotlivých prutů. Trám je obecné těleso v rovině a jako takové má tři stupně volnosti. Jeho obecná poloha proto bude určena třemi parametry - vodorovným posuvem
A. Změny délek od posuvu
Zvolíme si posuv Platí:
a tedy
Obdobně určíme
Vodorovný posuv se projeví i na prutech 3 a 4

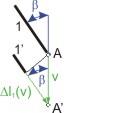
Na obrázku 3 je znázorněn způsob určení změny délky prutu č.1 , způsobené svislým posuvem
Podobně určíme i další změny délek
Zvolme si kladný smysl pootočení například podle obrázku 4. Bod A zůstává bez pohybu, proto
Bod C se posune svisle o hodnotu
Na základě rovnic (8) až (15) můžeme souhrně napsat
Pro pruty musejí samozřejmě platit i fyzikální rovnice ve tvaru
Vztahy (1) až (3) a (16) až (23) tvoří soustavu jedenácti rovnic pro jedenáct neznámých. Neznámými veličinami jsou: Zpracoval: František Novotný |
|
|
|
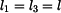
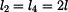
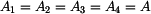
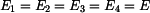
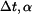

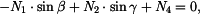
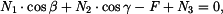
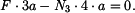
 , svislým posuvem
, svislým posuvem 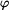 . Každý z těchto vlivů způsobí nějaké změny délek jednotlivých prutů. Skutečná změna délky každého prutu je pak dána jako změny délky od
. Každý z těchto vlivů způsobí nějaké změny délek jednotlivých prutů. Skutečná změna délky každého prutu je pak dána jako změny délky od 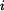 tedy můžeme psát:
tedy můžeme psát:
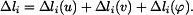
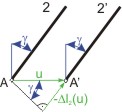
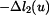 .
.
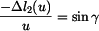
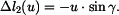
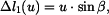
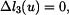
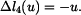
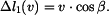
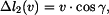
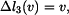
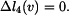
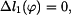
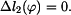
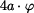 . Platí proto
. Platí proto
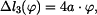
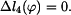
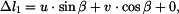
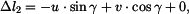
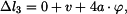
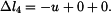
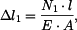
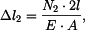
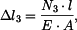
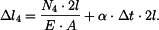
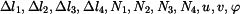 .
.