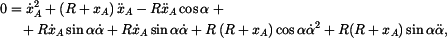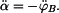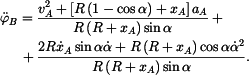|
KIN-05-3 Kinematika vázané soustavy hmotných bodů
Bod  se pohybuje po přímkové trajektorii se pohybuje po přímkové trajektorii 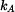 , bod , bod  po kružnici po kružnici  .
Vazba je realizována lanem, vedeným po oblouku kružnice .
Vazba je realizována lanem, vedeným po oblouku kružnice  . Výchozí polohy bodů jsou označeny . Výchozí polohy bodů jsou označeny  , , . .

Dáno:
konstanty  , , 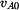 ; ;
rychlost bodu 
Určit:
délku lana 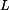 ; ;
zrychlení 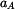 bodu bodu  ; ;
kinematické veličiny bodu  : :
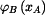 , , 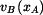 , , 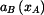 . .
Řešení:
Délka lana 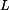 je dána délkou oblouku mezi body je dána délkou oblouku mezi body 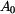 , , 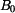 . .
Zrychlení bodu  . Protože rychlost . Protože rychlost 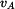 je dána jako funkce dráhy je dána jako funkce dráhy 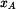 , použijeme vztah , použijeme vztah
Poloha bodu  je na kružnici je na kružnici 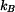 jednoznačně určena polohovým úhlem jednoznačně určena polohovým úhlem 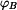 .
Určíme jej z vazebné podmínky pro délku lana .
Určíme jej z vazebné podmínky pro délku lana
takže
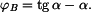 |
(1) |
Pro pomocný úhel  platí platí
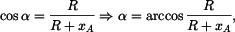 |
(2) |
takže
To ale platí, jen pokud část lana leží na oblouku kružnice 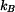 . Tedy jen pokud (podle obrázku) . Tedy jen pokud (podle obrázku)
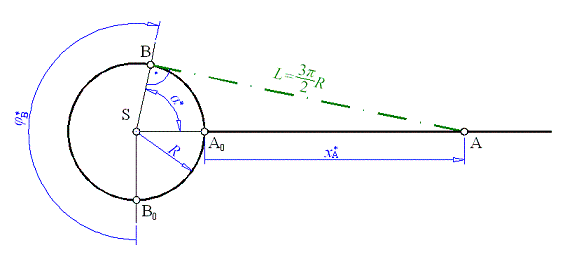
Omezení pro 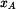 tak vychází tak vychází
Pro 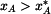 se situace změní. se situace změní.
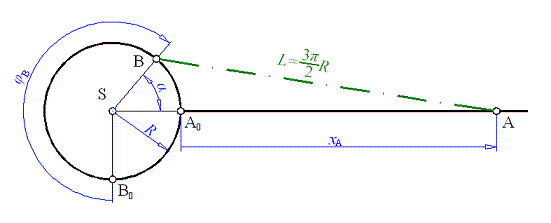
Kosinová věta pro obecný 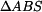 je je
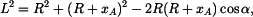 |
(3) |
takže
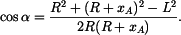 |
(4) |
Protože
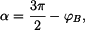 |
(5) |
je
Nakonec úplný výsledek
Další kinematické veličiny vyjádříme v souřadnicovém syslému "tečna, normála".
Rychlost bodu  je derivace proběhnuté dráhy podle času je derivace proběhnuté dráhy podle času
Proběhnutá dráha je v našem případě délka oblouku 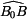 , tedy , tedy
Je tedy
Časovou derivaci 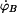 určíme implicitním derivováním. Pro určíme implicitním derivováním. Pro 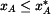 budeme derivovat vztahy (1) a (2). budeme derivovat vztahy (1) a (2).
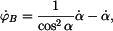 |
(6) |
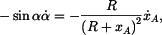 |
(7) |
takže
přičemž  závisí na závisí na 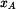 podle (2). podle (2).
Pro 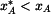 budeme derivovat (3) a (5) s výsledkem budeme derivovat (3) a (5) s výsledkem
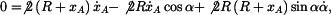 |
(8) |
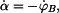 |
(9) |
takže
přičemž  závisí na závisí na 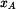 podle (4). Nakonec po úpravě a dosazení podle (4). Nakonec po úpravě a dosazení
kde
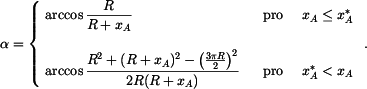
|
(10) |
Zrychlení bodu  má složku normálovou má složku normálovou 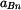 a tečnou a tečnou 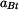 .
Protože poloměr křivosti kružnice je .
Protože poloměr křivosti kružnice je  , platí pro normálovou složku , platí pro normálovou složku
neboli
když pro  opět platí (10). opět platí (10).
Tečná složka zrychlení je derivace 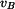 podle času, tj. podle času, tj.
Pro 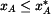 budeme derivovat (6) a (7) budeme derivovat (6) a (7)
Po úpravě a dosazení 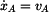 , , 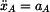 máme máme
V intervalu 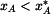 derivujeme (8) a (9). derivujeme (8) a (9).
Z toho po úpravě a dosazení
| 


 se pohybuje po přímkové trajektorii
se pohybuje po přímkové trajektorii 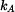 , bod
, bod  po kružnici
po kružnici 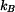 .
Vazba je realizována lanem, vedeným po oblouku kružnice
.
Vazba je realizována lanem, vedeným po oblouku kružnice 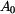 ,
,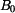 .
.
 ,
, 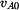 ;
;
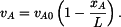
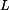 ;
;
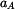 bodu
bodu 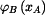 ,
, 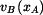 ,
, 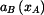 .
.
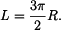
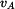 je dána jako funkce dráhy
je dána jako funkce dráhy 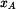 , použijeme vztah
, použijeme vztah
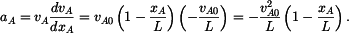
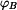 .
Určíme jej z vazebné podmínky pro délku lana
.
Určíme jej z vazebné podmínky pro délku lana
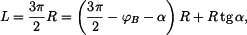
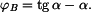
 platí
platí
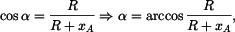
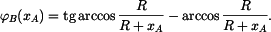
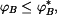
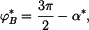
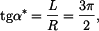
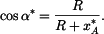
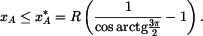
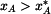 se situace změní.
se situace změní.
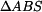 je
je
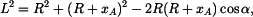
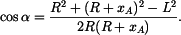
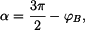

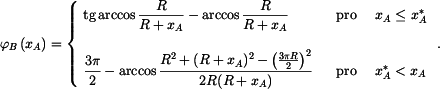
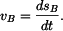
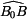 , tedy
, tedy
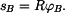
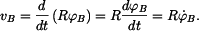
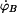 určíme implicitním derivováním. Pro
určíme implicitním derivováním. Pro 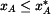 budeme derivovat vztahy (1) a (2).
budeme derivovat vztahy (1) a (2).
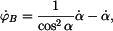
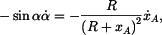
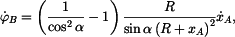
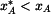 budeme derivovat (3) a (5) s výsledkem
budeme derivovat (3) a (5) s výsledkem
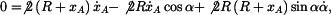
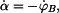

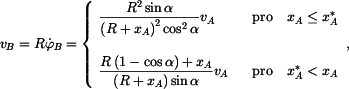
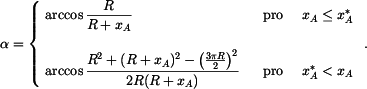
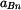 a tečnou
a tečnou 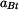 .
Protože poloměr křivosti kružnice je
.
Protože poloměr křivosti kružnice je 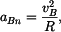
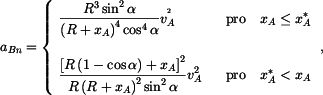
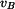 podle času, tj.
podle času, tj.
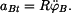
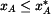 budeme derivovat (6) a (7)
budeme derivovat (6) a (7)
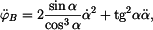
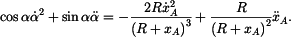
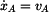 ,
, 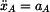 máme
máme
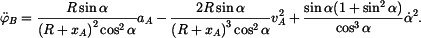
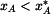 derivujeme (8) a (9).
derivujeme (8) a (9).