|
Navigace |
|
|
|
|
|
|
KIN-05-2 Kinematika vázané soustavy HB - vazba tyčí délky L
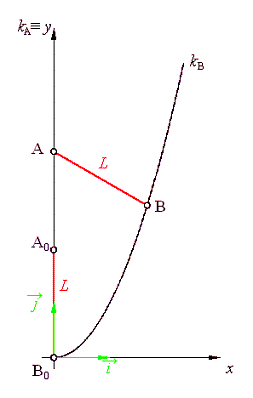 HB
HB  se pohybuje po vetikální přímce, která je osou parabolické trajektorie HB se pohybuje po vetikální přímce, která je osou parabolické trajektorie HB  . .
Dáno: Konstanty 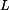 , , 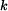 , ,  , ,
rovnice trajektorie 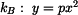 , ,
rychlost HB 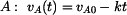 , ,
počáteční podmínka pro 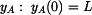
Určit: Kinematické veličiny 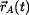 , , 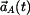 HB HB  . .
Kinematické veličiny 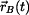 , , 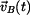 , , 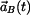 HB HB  . .
Hodnotu 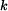 tak, "aby se tyč nepřetrhla". tak, "aby se tyč nepřetrhla".
Řešení: Polohový vektor 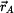 bodu bodu  . .
Složku (souřadnice) 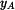 určíme z diferenciální rovnice určíme z diferenciální rovnice
separací
a integrací
s výsledkem
Zrychlení 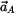 bodu bodu 
určíme jako
kde
Tedy
Polohový vektor 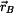 bodu bodu 
Protože se bod  pohybuje po dané trajektorii pohybuje po dané trajektorii 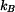 , platí , platí
Současně platí vazebná rovnice, vyjadřující konstantní ( = L ) vzdálenost bodu  od bodu od bodu 
Dosadíme za 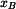 z rovnice (1) a upravíme z rovnice (1) a upravíme
To je kvadratická rovnice pro 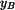 . .
Standartní tvar je
Řešením rovnice jsou kořeny
Platný kořen je ten s menší hodnotou 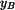 . Tedy po úpravě . Tedy po úpravě
a z rovnice (1)
Pozn.: Do výsledků pro 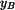 , , 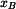 není nutno zavádět vypočtenou funkci není nutno zavádět vypočtenou funkci 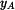 . Při pozdějším derivování je ale třeba na časovou proměnnost . Při pozdějším derivování je ale třeba na časovou proměnnost 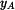 pamatovat. pamatovat.
Rychlost bodu  je vektor je vektor
přičemž
Derivace určíme implicitním derivováním, nejprve vztahu (3).
Z toho vypočteme
x - ovou složku rychlosti bodu  určíme z (2): určíme z (2):
takže
Zrychlení 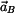 bodu bodu 
je vektor
kde
Obě derivace opět určíme implicitním derivováním. Nejprve vztahu (5) (po dělení 2)
Neznámá je  , takže , takže
neboli
Ze vztahu (6) nakonec
a z toho
neboli
Určení 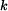 , "aby se tyč nepřetrhla ". , "aby se tyč nepřetrhla ".
Vazebnou podmínku, aby vzdálenost bodů  a a  byla byla 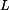 , lze splnit jen když , lze splnit jen když 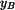 vypočtené z (4) je reálné číslo. To znamená, že člen pod odmocninou musí být kladný. vypočtené z (4) je reálné číslo. To znamená, že člen pod odmocninou musí být kladný.
Tedy
Tato nerovnost je splněna, když
neboli také když
Maximum 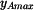 pro pro 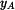 podle (1) nastává v čase podle (1) nastává v čase 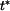 , kdy , kdy
Z toho
takže podle (1)
Řešením nerovnosti (7) pro 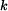 pak je pak je
Zpracoval: Arnošt Loos |
|
|
|
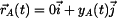
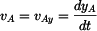
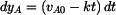
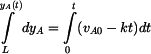
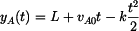 ,
,
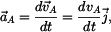
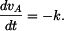
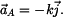
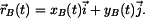
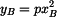
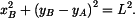
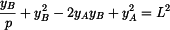
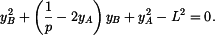
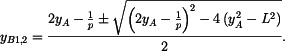
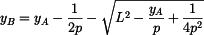

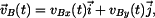
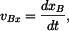
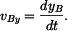
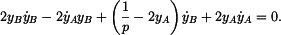
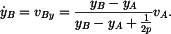
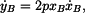
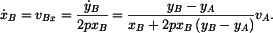
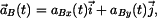
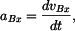
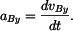
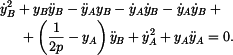
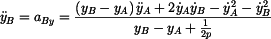
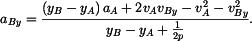
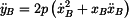
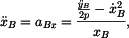
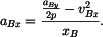
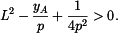
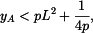
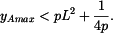
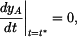

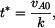
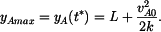
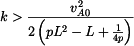 .
.