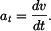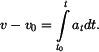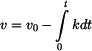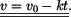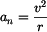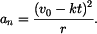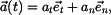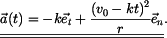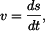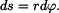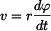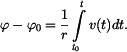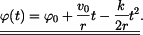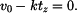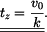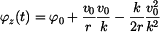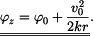|
Navigace |
|
|
|
|
|
|
TF-KS-01 - Křivočarý pohyb bodu
Bod se pohybuje se zrychlením 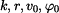
Určit: 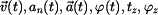
Řešení: Pro tečné zrychlení 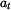 platí platí
Pro určení rychlosti lze odvodit vztah
Po dosazení
a integraci
Normálové zrychlení dosazením do vztahu
vyjde
Celkové zrychlení vyjádřené jako vektor
takže
Pro určení 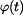 vyjdeme ze vztahu pro určení délky dráhy vyjdeme ze vztahu pro určení délky dráhy 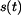
do něhož za 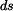 dosadíme dosadíme
Rychlost je dána jako
a pro určení 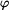 vyjde vztah vyjde vztah
Po dosazení za  z rovnice z rovnice 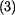 a integraci vyjde a integraci vyjde
Čas zastavení 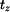 vypočteme ze vztahu vypočteme ze vztahu 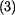 pro pro 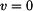 (zastavení) (zastavení)
Pak
Dosazením do 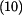 za za 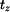 dostáváme dostáváme
a po úpravě
Zobrazení vektorů 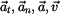 je na obr. 1. je na obr. 1.
Zpracoval: Radek Zbončák |
|
|
|
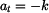 po kružnici o poloměru
po kružnici o poloměru  Počáteční rychlost bodu v čase
Počáteční rychlost bodu v čase 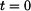 je
je 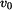 a poloha bodu je
a poloha bodu je 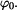 Určete
Určete 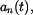
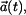
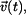
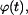 dobu zastavení
dobu zastavení 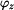 v okamžiku zastavení. Vektory rychlosti a zrychlení načrtněte.
v okamžiku zastavení. Vektory rychlosti a zrychlení načrtněte.