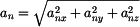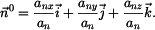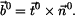|
Navigace |
|
|
|
|
|
|
KIN-04-2 HB v prostoru, vázaný na křivku danou parametricky
Dáno: Konstanty  , ,  , , 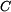 , , 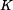 , , 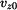 ; ;trajektorie HB (eliptická šroubovice)
rychlost ve směru osy
a počáteční podmínka pro
Určit:
Řešení:
Protože
To je diferenciální rovnice pro Zapsaná v separovaném tvaru je
Připojíme integrační symboly se sobě odpovídajícími mezemi
a výsledek integrace je
Hodnotu
je
Z toho vyplývá, že
Pro souřadnice pak stačí napsat
Složky rychlosti jsou
a složky zrychlení
přičemž
a
Absolutní hodnota rychlosti je
a absolutní hodnota zrychlení
Vektor rychlosti leží na tečně k trajektorii, takže platí
Jednotkový tečný vektor je tedy
Zrychlení má složku tečnou a normálnou. Tečnou složku vypočteme jako průmět vektoru
Protože je
bude
Označíme-li jednotlivé kartézské složky vektoru
a jednotkový vektor v normálném směru
Nakonec jednotkový vektor v binormálném směru je
Zpracoval: Jan Blažek |
|
|
|
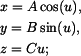
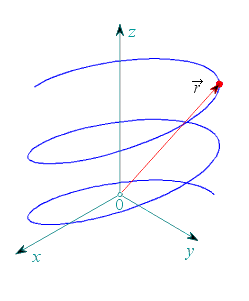
 jako funkce času
jako funkce času
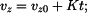
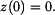
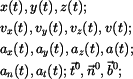
 , musí platit
, musí platit
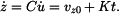
 .
.
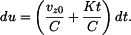
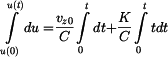
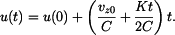
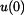 zatím neznáme. Určíme ji z počáteční podmínky pro
zatím neznáme. Určíme ji z počáteční podmínky pro 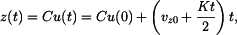
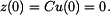
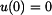 a
a

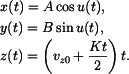
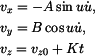
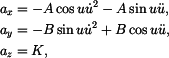
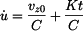
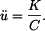
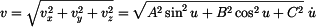
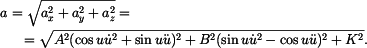
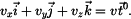
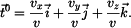
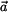 do směru tečny, tedy
do směru tečny, tedy

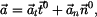
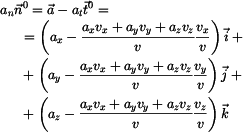
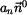 jako
jako 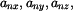 bude
bude