|
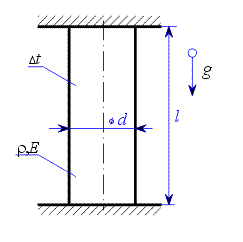
Sloup v tíhovém poli a změna teploty
 |
 |
| Obr. 1 |
Dáno : 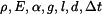 . .
Určete : průběh napětí, reakce a poměrné deformace v tyči. Anylyzujte vliv velikosti a znaménka 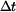 na výsledek. na výsledek.
Tyč o délce 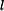 je upevněna podle obrázku 1 a poté se její teplota změní o je upevněna podle obrázku 1 a poté se její teplota změní o 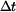 . .
Řešení :
 |
 |
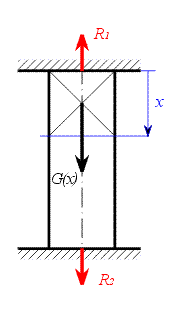
| Obr. 2 |
Zavedeme reakce a souřadnici  - viz obr. 2. Pro soustavu sil ležících v přímce napíšeme
jedinou rovnici rovnováhy - viz obr. 2. Pro soustavu sil ležících v přímce napíšeme
jedinou rovnici rovnováhy
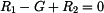 . .
|
(1) |
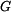 představuje tíhu celé tyče představuje tíhu celé tyče
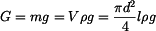 . .
|
(2) |
Úloha je jednou staticky neurčitá, musíme proto formulovat deformační rovnici. Vzhledem k uložení obou konců
tyče musí platit
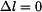 . .
|
(3) |
Hodnotu 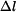 získáme integrací poměrné deformace získáme integrací poměrné deformace
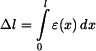 . .
|
(4) |
Tyč se deformuje nejen působením vnějších sil, ale také v důsledku změny teploty 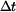 . Poměrná deformace . Poměrná deformace  se skládá z komponenty způsobené silami
se skládá z komponenty způsobené silami 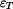 a z komponenty způsobené změnou teploty a z komponenty způsobené změnou teploty 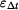 : :
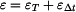 . .
|
(5) |
Pro 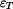 platí platí
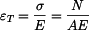 , ,
|
(6) |
kde 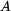 je průřez : je průřez : 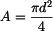 . .
Pro 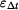 platí platí
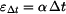 . .
|
(7) |
Vztah (4) vypadá po dosazení takto :
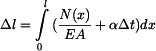 . .
|
(8) |
Vnitřní sílu 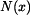 stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici  (viz. obr. 2), působí
tahem reakce (viz. obr. 2), působí
tahem reakce  a tlakem tíha a tlakem tíha 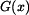 části nad řezem. části nad řezem.
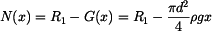 . .
|
(9) |
Z poslední rovnice dosadíme do (8) a (3) a po integraci dostáváme
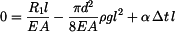 . .
|
(10) |
Vyjádříme reakci 
 . .
|
(11) |
Z rovnice rovnováhy (1) stanovíme 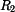 : :
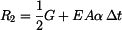 . .
|
(12) |
Z (11) dosadíme  do (9) a pro napětí pak platí do (9) a pro napětí pak platí
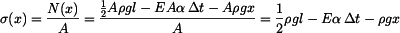 . .
|
(13) |
Analyzujme nyní velikost reakcí v závislosti na 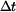 . .
Pokud je 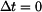 , pak , pak 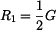 a a 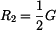 . .
 |
 |
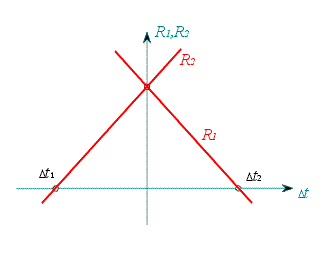
| Obr. 3 |
Lineární závislost reakcí na 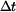 znázorňuje obr. 3. znázorňuje obr. 3.
Je-li 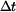 uvnitř intervalu uvnitř intervalu 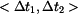 , pak obě reakce míří nahoru. Pro , pak obě reakce míří nahoru. Pro 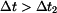 se mění znaménko u se mění znaménko u  , která
pak míří dolů. , která
pak míří dolů.
Naopak pro 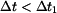 se obrací znaménko a tedy i směr reakce se obrací znaménko a tedy i směr reakce 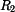 . .
Stanovme nyní hodnoty 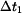 a a 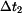 . .
Pro 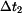 , platí že , platí že 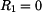 : :
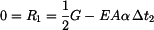 , ,
|
(14) |
čili
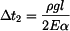 . .
|
(15) |
Pro 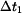 platí, že platí, že 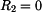 : :
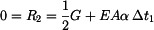
|
(16) |
a tedy
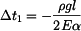 . .
|
(17) |
 |
 |
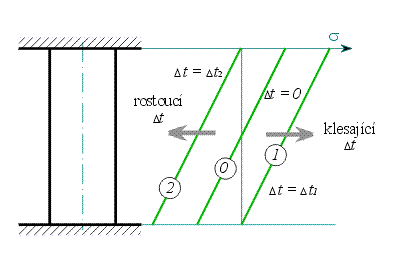
| Obr. 4 |
Podívejme se nyní na průběh napětí (vztah (13)). Pro 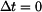 dostaneme závislost označenou v obr.4 číslem dostaneme závislost označenou v obr.4 číslem 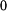 . .
S rostoucím 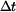 se průběh posouvá směrem doleva až při se průběh posouvá směrem doleva až při 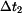 dosáhne nulové hodnoty na horním konci tyče - průběh dosáhne nulové hodnoty na horním konci tyče - průběh 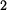 . .
S klesajícím 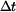 se průběh posouvá doprava a pro se průběh posouvá doprava a pro 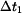 dosáhne nuly na dolním konci tyče - průběh dosáhne nuly na dolním konci tyče - průběh 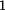 . .
S dalším růstem, resp. poklesem teploty se průběhy posunují dál doleva resp. doprava.
Je-li 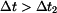 , pak je napětí v celé tyči záporné, tedy tlakové. , pak je napětí v celé tyči záporné, tedy tlakové.
Je-li 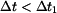 , je napětí v celé tyči kladné - tahové. , je napětí v celé tyči kladné - tahové.
Je-li 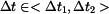 , je napětí v části tyče tahové a v části tlakové. , je napětí v části tyče tahové a v části tlakové.
| 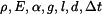 .
.

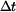 na výsledek.
na výsledek.
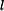 je upevněna podle obrázku 1 a poté se její teplota změní o
je upevněna podle obrázku 1 a poté se její teplota změní o 
 - viz obr. 2. Pro soustavu sil ležících v přímce napíšeme
jedinou rovnici rovnováhy
- viz obr. 2. Pro soustavu sil ležících v přímce napíšeme
jedinou rovnici rovnováhy
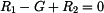 .
.
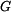 představuje tíhu celé tyče
představuje tíhu celé tyče
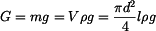 .
.
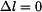 .
.
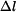 získáme integrací poměrné deformace
získáme integrací poměrné deformace
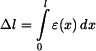 .
.
 se skládá z komponenty způsobené silami
se skládá z komponenty způsobené silami 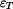 a z komponenty způsobené změnou teploty
a z komponenty způsobené změnou teploty 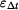 :
:
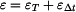 .
.
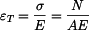 ,
,
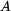 je průřez :
je průřez : 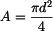 .
.
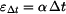 .
.
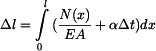 .
.
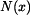 stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici
stanovíme metodou řezu. Provedeme-li myšlený řez na souřadnici  a tlakem tíha
a tlakem tíha 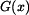 části nad řezem.
části nad řezem.
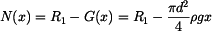 .
.
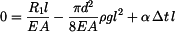 .
.
 .
.
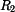 :
:
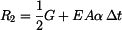 .
.
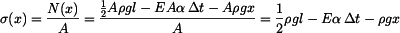 .
.
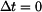 , pak
, pak 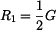 a
a 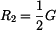 .
.

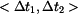 , pak obě reakce míří nahoru. Pro
, pak obě reakce míří nahoru. Pro 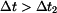 se mění znaménko u
se mění znaménko u 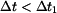 se obrací znaménko a tedy i směr reakce
se obrací znaménko a tedy i směr reakce 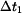 a
a 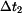 .
.
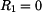 :
:
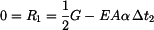 ,
,
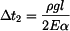 .
.
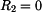 :
:
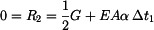
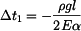 .
.

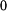 .
.
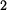 .
.
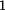 .
.
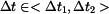 , je napětí v části tyče tahové a v části tlakové.
, je napětí v části tyče tahové a v části tlakové.