|
Navigace |
|
|
|
|
|
|
Průhyb nosníku s nelineárním materiálem
Určete maximální napětí a průhyb nosníku. Nosník má obdélníkový průřez a materiál je elastický a má nelineární tahový diagram. Předpokládejte malé deformace.
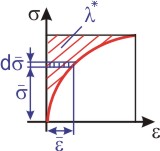
Za předpokladu, že průřezy nosníku zůstavají po deformaci rovinné a kolmé ke střednici (Bernoulliho hypotéza), bude prodloužení lineární funkcí
Označme maximální prodloužení v řezu o souřadnici
a napětí po dosazení do vztahu
Moment přenášený v průřezu vypočteme jako moment vnitřních sil k ose y
Dosaďme ze vztahu
Maximální napětí bude v krajním vlákně uprostřed nosníku:
Výraz
K výpočtu průhybu uprostřed nosníku použijeme 2. Castiglianovu větu. Zatížíme nosník uprostřed fiktivní silou
Vnitřní moment v nosníku pak bude
a jeho derivace podle
Stanovte nejprve hustotu doplňkové deformační energie
po dosazení do
a po dosazení za
Průhyb je samozřejmě nelineární (v tomto případě kvadratickou) funkcí zatížení. Ke stejnému výsledku bychom došli integrací diferenciální rovnice průhybové čáry
kterou dostaneme ze vztahu
Zvídavý student se o tom rád předsvědčí. Zpracoval: František Novotný |
|
|
|
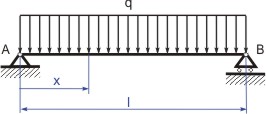
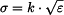
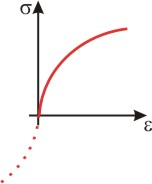
 stejně jako u nosníku,který se řídí lineárním Hookeovým zákonem. Napětí v průřezu však nebude lineární funkcí
stejně jako u nosníku,který se řídí lineárním Hookeovým zákonem. Napětí v průřezu však nebude lineární funkcí 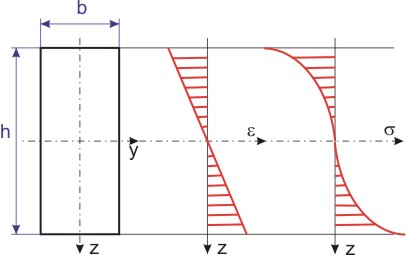
 jako
jako 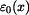 , pak prodloužení v průřezu bude popsáno funkcí
, pak prodloužení v průřezu bude popsáno funkcí
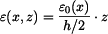
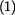 bude popsáno funkcí
bude popsáno funkcí
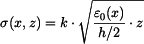
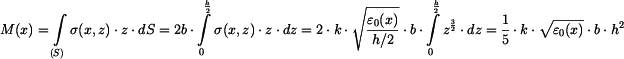
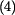 do
do 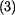 za
za
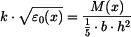
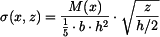
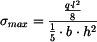
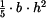 bychom mohli označit za ohybový modul průřezu nosníku obdélníkového průřezu s materiálem typu
bychom mohli označit za ohybový modul průřezu nosníku obdélníkového průřezu s materiálem typu 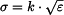 .
.
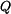 . Průhyb vypočteme derivací doplňkové deformační energie
. Průhyb vypočteme derivací doplňkové deformační energie 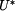 podle této síly, neboť v případě, kdy nejsou přítomny geometrické nelinearity je doplňková deformační energie rovna doplňkové práci vnějších sil
podle této síly, neboť v případě, kdy nejsou přítomny geometrické nelinearity je doplňková deformační energie rovna doplňkové práci vnějších sil  .
.
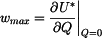
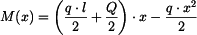
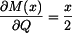
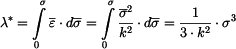
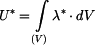
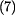 a derivaci složené funkce:
a derivaci složené funkce:
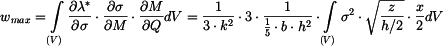
 ze vztahu
ze vztahu 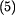 a
a  pro
pro 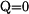 a
a 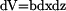 dostaneme:
dostaneme:
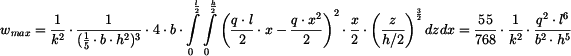
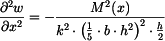
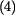 po dosazení za
po dosazení za