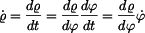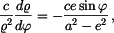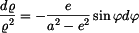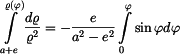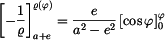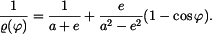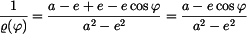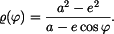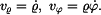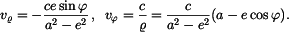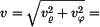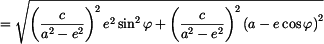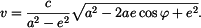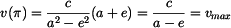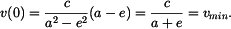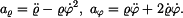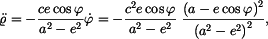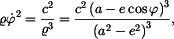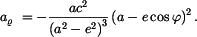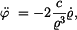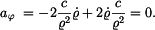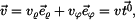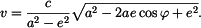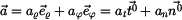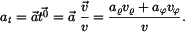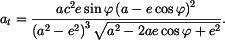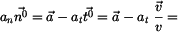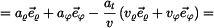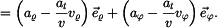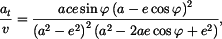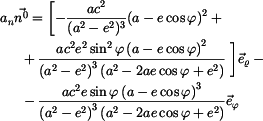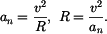|
|
KIN-03-2 Volný pohyb hmotného bodu ve 2D
Dáno: V polárních souřadnicích 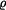 , , 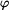 je pohyb hmotného bodu určen vztahy je pohyb hmotného bodu určen vztahy
kde  , ,  , ,  jsou dané konstanty. jsou dané konstanty.
Určit: Rovnici 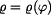 trajektorie HB, složky trajektorie HB, složky 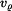 , , 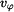 rychlosti a složky rychlosti a složky 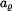 , , 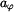 zrychlení při počátečních podmínkách zrychlení při počátečních podmínkách
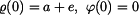 . .
|
Řešení:
Úpravou definičního vztahu pro 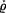
a dosazením zadání dostaneme
což lze separovat do tvaru
a integrovat v odpovídajících mezích
s výsledkem
neboli
Úprava
neboli
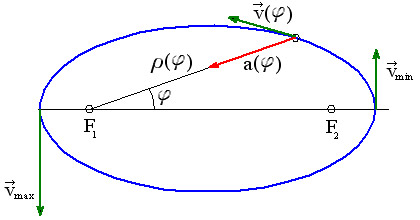
To je rovnice elipsy s ohniskem v počátku polárních souřadnic 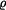 , , 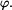
Pro složky rychlosti v polárních souřadnicích platí
V daném případě tedy
Absolutní hodnota rychlosti je
což je
Největší je rychlost pro 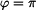
a nejmenší je rychlost pro 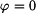
Pro složky zrychlení v polárních souřadnicích platí
V daném případě je
takže po dosazení
Dále
takže
Zrychlení má tedy jen radiální složku, orientovanou do středu polárních souřadnic. Jedná se o tzv. centrální pohyb, který konají např. planety okolo Slunce.
 |
 |
| Obr.1 Volný pohyb hmotného bodu ve 2D |
Vyšetříme ještě složky vektorů 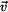 a a 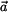 v přirozeném souřadnicovém systému s bází v přirozeném souřadnicovém systému s bází  , , 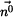
Platí
přičemž absolutní hodnota (viz. výše) je
Analogicky platí
Tečnou složku zrychlení vypočteme jako průmět vektoru 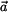 do do 
V našem případě tedy tečná složka
Normálová složka zrychlení pak bude
V daném případě je po úpravě
takže po dosazní za 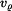 , , 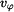 , , 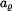 , , 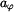 máme máme
Samotná hodnota 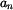 je nakonec absolutní hodnotou vektoru na pravé straně. Znalost hodnoty je nakonec absolutní hodnotou vektoru na pravé straně. Znalost hodnoty 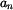 navíc umožní výpočet poloměru křivosti navíc umožní výpočet poloměru křivosti  eliptické trajektorie v příslušném bodě eliptické trajektorie v příslušném bodě
Zpracoval: Arnošt Loos
|
|
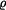 ,
, 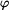 je pohyb hmotného bodu určen vztahy
je pohyb hmotného bodu určen vztahy
 ,
,  ,
,  jsou dané konstanty.
jsou dané konstanty.
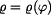 trajektorie HB, složky
trajektorie HB, složky 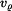 ,
, 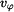 rychlosti a složky
rychlosti a složky 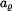 ,
, 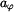 zrychlení při počátečních podmínkách
zrychlení při počátečních podmínkách
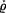
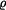 ,
, 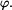
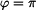
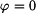
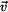 a
a 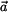 v přirozeném souřadnicovém systému s bází
v přirozeném souřadnicovém systému s bází  ,
, 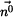
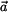 do
do 
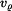 ,
, 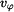 ,
, 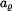 ,
, 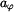 máme
máme
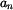 je nakonec absolutní hodnotou vektoru na pravé straně. Znalost hodnoty
je nakonec absolutní hodnotou vektoru na pravé straně. Znalost hodnoty 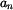 navíc umožní výpočet poloměru křivosti
navíc umožní výpočet poloměru křivosti  eliptické trajektorie v příslušném bodě
eliptické trajektorie v příslušném bodě
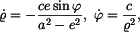
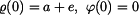 .
.