|
Příklad 2.
Tenký kotouč podle obr. 1 byl při teplotě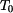 bez napětí. Jeho čelní plochy jsou teplotně izolovány, ale nic nebrání v jejich volné dilataci. Tento kotouč byl zvolna zahřát tak, že vznikne ustálený tepelný stav, kdy na vnitřním okraji kotouče je teplota bez napětí. Jeho čelní plochy jsou teplotně izolovány, ale nic nebrání v jejich volné dilataci. Tento kotouč byl zvolna zahřát tak, že vznikne ustálený tepelný stav, kdy na vnitřním okraji kotouče je teplota 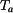 a na vnějším okraji kotouče je teplota a na vnějším okraji kotouče je teplota 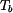 . Jaké je napětí v kotouči? . Jaké je napětí v kotouči?
Dáno: 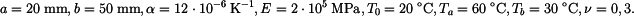
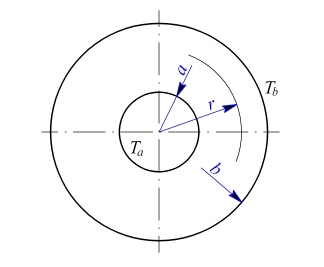
Obr. 1
Řešení: V kotouči vzniká ustálené teplotní pole, které je osově symetrické, teplota se po tloušťce kotouče nemění. Jedná se o rovinnou napjatost - nevznikne osové napětí. Rovnice vedení tepla má v tomto případě tvar
Za vztažný poloměr zvolíme vnější poloměr kotouče 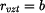 . Řešení této rovnice je funkcí teploty . Řešení této rovnice je funkcí teploty
kde integrační konstanty 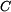 a a 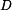 určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
Odtud
Diferenciální rovnice pro radiální posuv v případě rovinné napjatosti:
Z homogenního řešení 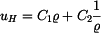 dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
kde integrační konstanty  a a  určujeme z podmínek na okraji kotouče. určujeme z podmínek na okraji kotouče.
Diferenciální rovnici pro radiální posuv vynásobíme  a dosadíme za funkci a dosadíme za funkci 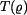 . Na pravé straně dostáváme: . Na pravé straně dostáváme: 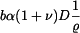 . Označme . Označme  . Partikulární řešení bude v tomto případě . Partikulární řešení bude v tomto případě
a napětí z tohoto řešení odvozená jsou
Sečtěme homogenní řešení a partikulární řešení a přidáme teplotní člen 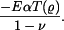 Dostaneme napětí Dostaneme napětí
Integrační konstanty  a a  určíme z podmínek pro volné okraje: určíme z podmínek pro volné okraje:
Po dosazení
Rovnice můžeme dále upravovat a konstanty A a B vyjádřit obecně pro tento typ zatížení a okrajových podmínek. Rozumnější bude v této fázi konstanty, které mají rozměr napětí, vypočítat numericky. Vyjde 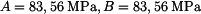 . Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru. . Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.
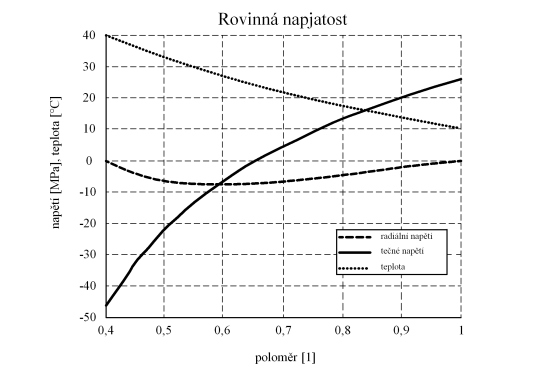
Obr. 2
Kdybychom zabránili volné změně tloušťky kotouče, vzniklo by v kotouči osové napětí 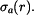 Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak 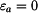 a jedná se o tzv. rovinnou deformaci. Určíme napětí a jedná se o tzv. rovinnou deformaci. Určíme napětí 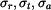 v tomto případě. Pro poměrné deformace máme nyní vztahy v tomto případě. Pro poměrné deformace máme nyní vztahy
Z poslední rovnice získáme 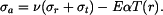
Na pravé straně diferenciální rovnice pro radiální posuv  je v případu rovinné deformace výraz je v případu rovinné deformace výraz
Zde obdobně zavedeme 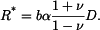
Z homogenního řešení rovnice 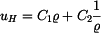 máme opět máme opět
(konstanty 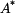 a a 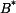 mají jinou hodnotu, než mají jinou hodnotu, než  a a  v předchozím řešení). v předchozím řešení).
Partikulární řešení
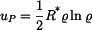 dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost): dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
K součtu jednotlivých částí napětí musíme ještě připojit teplotní člen 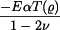 : :
Axiální napětí bude
Z podmínek na okrajích kotouče 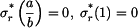 určíme konstanty určíme konstanty 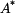 a a 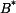 , které dosadíme do vztahů pro napětí, pak , které dosadíme do vztahů pro napětí, pak
Průběh napětí je na obr. 3.
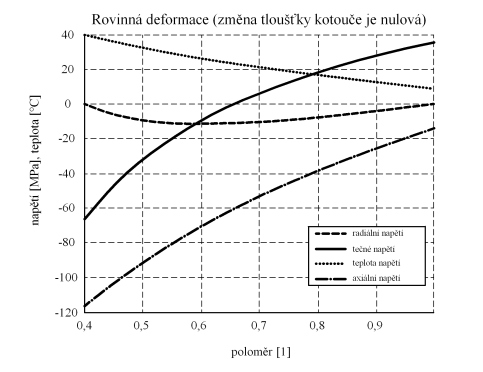
Obr. 3
Pozn.: Vztahy pro napětí 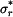 a a 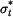 v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy 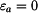 ) můžeme dostat přímo ze vztahů ) můžeme dostat přímo ze vztahů 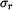 a a 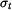 pro rovinnou napjatost (volná dilatace tloušťky pro rovinnou napjatost (volná dilatace tloušťky 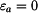 ), jestliže do nich dosadíme za Youngův modul ), jestliže do nich dosadíme za Youngův modul 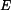 vztah vztah 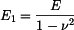 , za teplotní roztažnost , za teplotní roztažnost  vztah vztah 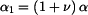 a za Poissonovu konstantu a za Poissonovu konstantu  vztah vztah 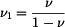 . (Je třeba dosadit i do výrazu pro konstantu . (Je třeba dosadit i do výrazu pro konstantu  .) .)
zpracoval:Miroslav Denk
| 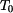 bez napětí. Jeho čelní plochy jsou teplotně izolovány, ale nic nebrání v jejich volné dilataci. Tento kotouč byl zvolna zahřát tak, že vznikne ustálený tepelný stav, kdy na vnitřním okraji kotouče je teplota
bez napětí. Jeho čelní plochy jsou teplotně izolovány, ale nic nebrání v jejich volné dilataci. Tento kotouč byl zvolna zahřát tak, že vznikne ustálený tepelný stav, kdy na vnitřním okraji kotouče je teplota 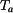 a na vnějším okraji kotouče je teplota
a na vnějším okraji kotouče je teplota 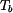 . Jaké je napětí v kotouči?
. Jaké je napětí v kotouči?
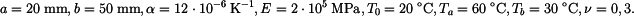

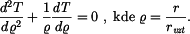
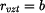 . Řešení této rovnice je funkcí teploty
. Řešení této rovnice je funkcí teploty
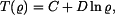
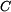 a
a 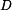 určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
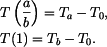
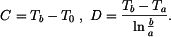
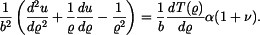
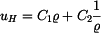 dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
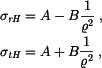
 a
a  určujeme z podmínek na okraji kotouče.
určujeme z podmínek na okraji kotouče.
 a dosadíme za funkci
a dosadíme za funkci 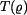 . Na pravé straně dostáváme:
. Na pravé straně dostáváme: 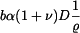 . Označme
. Označme  . Partikulární řešení bude v tomto případě
. Partikulární řešení bude v tomto případě
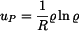
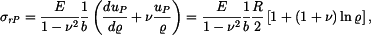
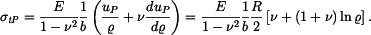
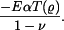 Dostaneme napětí
Dostaneme napětí
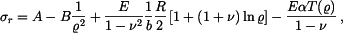
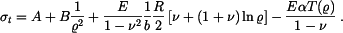
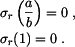
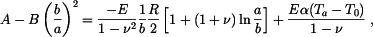

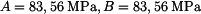 . Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.
. Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.

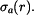 Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak
Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak 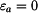 a jedná se o tzv. rovinnou deformaci. Určíme napětí
a jedná se o tzv. rovinnou deformaci. Určíme napětí 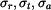 v tomto případě. Pro poměrné deformace máme nyní vztahy
v tomto případě. Pro poměrné deformace máme nyní vztahy
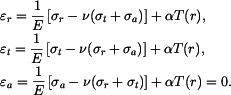
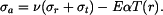
 je v případu rovinné deformace výraz
je v případu rovinné deformace výraz
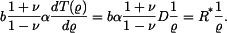
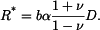
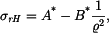
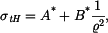
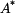 a
a 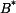 mají jinou hodnotu, než
mají jinou hodnotu, než 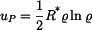 dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
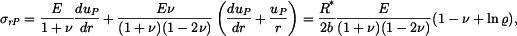
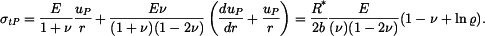
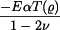 :
:
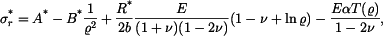
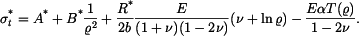
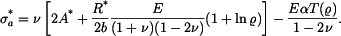
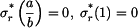 určíme konstanty
určíme konstanty 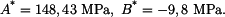

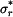 a
a 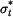 v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy
v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy 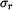 a
a 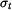 pro rovinnou napjatost (volná dilatace tloušťky
pro rovinnou napjatost (volná dilatace tloušťky 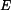 vztah
vztah 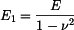 , za teplotní roztažnost
, za teplotní roztažnost  vztah
vztah 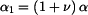 a za Poissonovu konstantu
a za Poissonovu konstantu  vztah
vztah 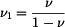 . (Je třeba dosadit i do výrazu pro konstantu
. (Je třeba dosadit i do výrazu pro konstantu  .)
.)