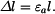Teplotní napětí v tyčích namáhaných na tah nebo tlak
Příklad 1.
Ocelová kolejnice nekonečné délky se ochladí z počáteční teploty
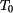
, při které byla bez napětí, o teplotu
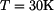
. Jaké napětí vznikne v kolejnici, je-li
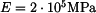
,
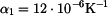
?
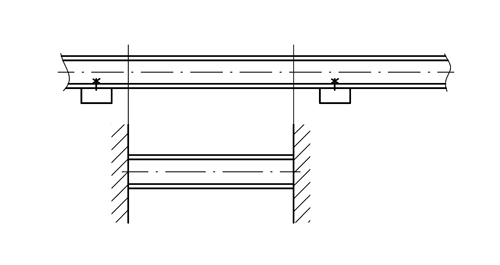
Řešení: Kolejnici můžeme považovat za ideálně vetknutou tyč. Při ochlazení v ní vznikne tahové napětí, které eliminuje teplotní deformaci 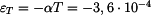 .
.
zpracoval:Miroslav Denk
Příklad 2.
Příklad 3.
Příklad 4.
Mějme vetknutou tyč konstantního průřezu podle obr. 1, změna teploty 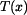 bude nyní funkcí souřadnice
bude nyní funkcí souřadnice  .
.
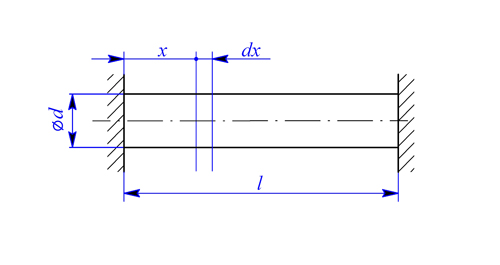
Obr. 1
Volné teplotní prodloužení elementu 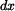 v místě
v místě  bude
bude
celkové volné prodloužení tyče vlivem teploty pak je
Ve vetknutích vznikne tlaková síla F, která by zkrátila tyč o
Prodloužení tyče od teploty a zkrácení vlivem reakce musí být stejné, sílu 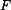 vypočteme z této podmínky
vypočteme z této podmínky
zpracoval:Miroslav Denk
Příklad 5.
Ocelová tyč a měděná trubka stejné délky jsou spojeny tuhými čely podle obr. 1. Jaké napětí vznikne v jednotlivých částech, ohřejeme-li soustavu o teplotu  ?
?
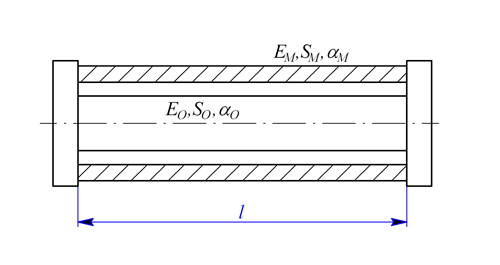
Obr. 1
Řešení: Teplotní roztažnost mědi je větší než teplotní roztažnost oceli ( ,
, 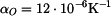 ). Prodloužení obou částí však musí být stejné. V trubce vznikne tlakové a v tyči tahové napětí. Deformační podmínka je
). Prodloužení obou částí však musí být stejné. V trubce vznikne tlakové a v tyči tahové napětí. Deformační podmínka je
Výsledné síly, kterými trubka a tyč působí na tuhá čela musí být stejně velké, ale opačného smyslu
zpracoval:Miroslav Denk
Z této podmínky rovnováhy a deformační podmínky, můžeme vypočítat napětí 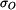 a
a 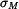 .
.
Příklad 6.
Příklad 7.
Všechny pruty soustavy podle obr. 1 jsou ze stejného materiálu a mají stejný průřez. Jaké bude v jednotlivých prutech napětí, ohřeje-li se
a) celá soustava o 
b) ohřeje-li se pouze prut 2 o 
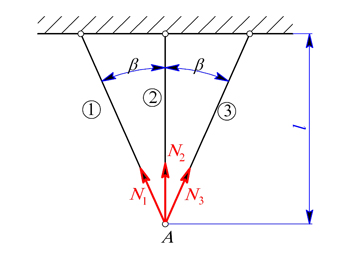
Obr. 1
Soustava je symetrická a 1-krát staticky neurčitá, tedy
Rovnice rovnováhy styčníku A je
Po deformaci styčník A zůstane na ose symetrie a deformační podmínka má tvar
a) prodloužení prutů jsou
Z deformační podmínky
a z rovnice rovnováhy vyjde
resp. 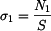 ,
, 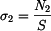
b) Soustava je stále symetrická, prodloužení prutů jsou
Z deformační podmínky
a z rovnice rovnováhy vyjde
resp. 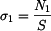 ,
, 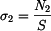
zpracoval:Miroslav Denk
Přibližný výpočet teplotních napětí v nosnících
Příklad 1.
Tyč obdélníkového průřezu podle obr. 1 je zatížena přírůstkem teploty, který má lineární průběh v závislosti na souřadnici z: 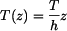 . Dáno:
. Dáno: 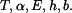 Určete napětí v tyči a deformaci tyče.
Určete napětí v tyči a deformaci tyče.
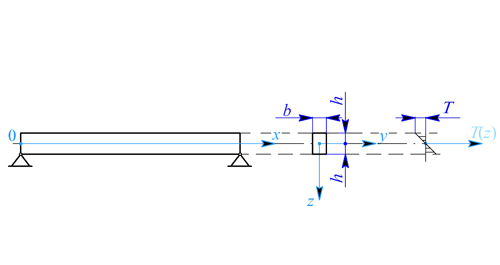
Obr. 1
Řešení:
V tyči nevznikne napětí (přírůstek teploty je lineární funkcí souřadnice  ).
).
Diferenciální rovnice průhybové čáry
Průhybová čára je kružnice s poloměrem 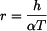 . Tyč se neprodlouží, neboť střední posuv průřezu je nulový:
. Tyč se neprodlouží, neboť střední posuv průřezu je nulový:
zpracoval:Miroslav Denk
Příklad 2.
Tyč z příkladu 1. je zatížena přírůstkem teploty, který má parabolický průběh (obr. 1) v závislosti na souřadnici  , určete napětí v tyči a její deformaci.
, určete napětí v tyči a její deformaci.
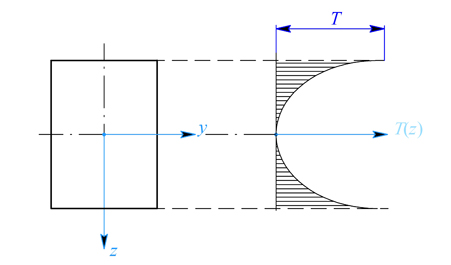
Obr. 1
Řešení:
Napětí má parabolický průběh (obr. 2). Tyč se neprohne, protože 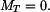
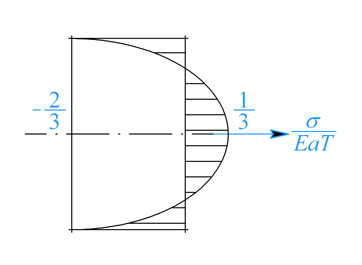
Obr. 2
Osový posuv v místě 
střední osový posuv
a celkové prodloužení tyče
zpracoval:Miroslav Denk
Příklad 3.
Tyč z příkladu 1. je zatížena přírůstkem teploty s parabolickým průběhem podle obr. 1. Určete napětí v tyči a její průhyb.
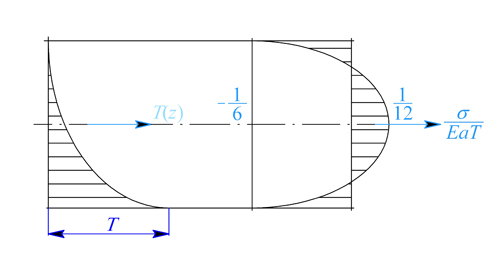
Obr. 1
Řešení:
Průhyb nosníku je dán diferenciální rovnicí
a po dosazení
Průhybová čára tedy bude kružnice o poloměru 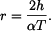
zpracoval:Miroslav Denk
Příklad 4.
Tyč z příkladu 1. je vetknutá na obou koncích podle obr. 1 a zatížena přírůstkem teploty
Jaké napětí vznikne v tyči a jaká bude její deformace?
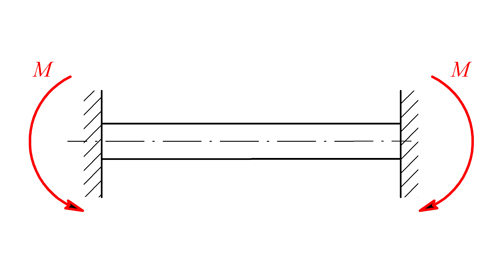
Obr. 1
Řešení: Tyč se neprohne, neboť z vetknutí se na ni budou přenášet ohybové momenty 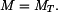 Napětí, které vznikne v tyči má lineární průběh
Napětí, které vznikne v tyči má lineární průběh
zpracoval:Miroslav Denk
Příklad 5.
Tyč z příkladu 1. je vetknutá na levém konci a na pravém konci prostě podepřena. Průběh přírůstku teploty je lineární funkcí souřadnice  . Určete napětí a deformaci tyče.
. Určete napětí a deformaci tyče.
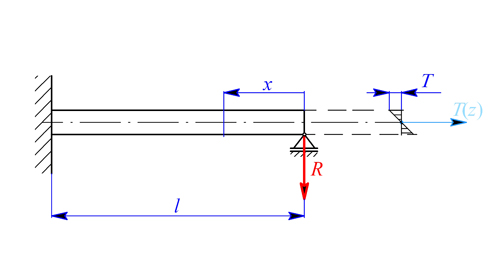
Obr. 1
Řešení:
Stále pro průběh teploty platí
V podpoře vznikne reakce  , která bude bránit průhybu nosníku směrem vzhůru. Moment v obecném řezu je
, která bude bránit průhybu nosníku směrem vzhůru. Moment v obecném řezu je
diferenciální rovnice má tvar
a řešení
Velikost reakce  a konstant
a konstant 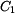 a
a 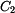 určíme z okrajových podmínek pro deformaci nosníku
určíme z okrajových podmínek pro deformaci nosníku
Odtud
Napětí v nosníku získáme superpozicí napětí v nosníku vetknutém na levém konci a zatíženém ohřevem (napětí nevzniká) a nosníku vetknutém na levém konci a na pravém konci zatíženém silou  .
.
Maximální napětí je ve vetknutí
zpracoval:Miroslav Denk
Příklad 6.
Nosník na třech podporách obdélníkového průřezu podle obr. 1 je zatížen přírůstkem teploty 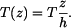 Určete napětí a deformaci nosníku.
Určete napětí a deformaci nosníku.
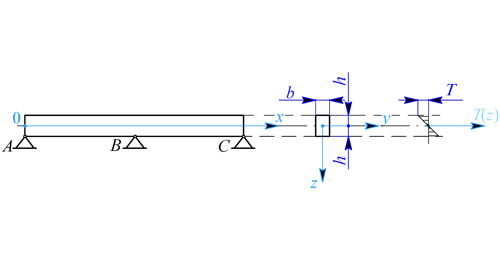
Obr. 1
Řešení: Pokud je nosník uložen na dvou podporách A a C, napětí v něm nevznikne a vlivem přírůstku teploty se prohne do kružnice. Poloměr kružnice
kde
tedy
Průhyb způsobený změnou teploty vypočteme pomocí obr. 2
Protože platí, že  , lze napsat
, lze napsat
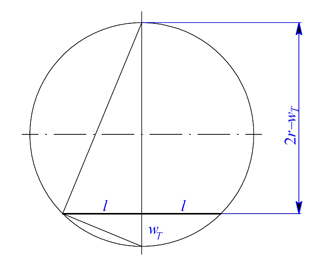
Obr. 2
Pro nosník zatížený silou rovnou reakci  uprostřed je průhyb (obr. 3)
uprostřed je průhyb (obr. 3)
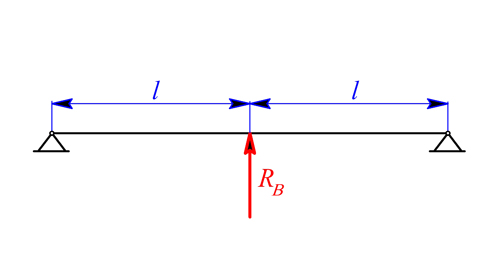
Obr. 3
Z podmínky  vyjde
vyjde
Maximální napětí je uprostřed nosníku:
Průhyb bude stejný jako u nosníku v příkladu 5. Reakce  je dvojnásobkem reakce
je dvojnásobkem reakce  z příkladu 5.
z příkladu 5.
zpracoval:Miroslav Denk
Příklad 7.
Mějme kompozitní nosník - tzv. bimetal - složený ze dvou částí z různých materiálů podle obr. 1. Určeme napětí a deformaci, ohřeje-li se celý nosník o teplotu  . Předpokládejme stejný průřez obou částí, moduly pružnosti
. Předpokládejme stejný průřez obou částí, moduly pružnosti 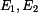 a součinitele teplotní roztažnosti
a součinitele teplotní roztažnosti 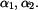
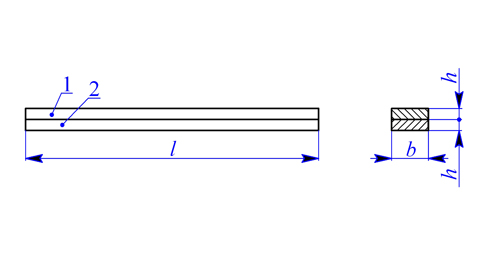
Obr. 1
Řešení: Po zahřátí se nosník prohne, průhybová čára bude kružnice. Předpokládejme, že zakřivení společné plochy bude 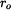 , dále předpokládejme, že vlivem ohřátí se společná plocha roztáhne v osovém směru o
, dále předpokládejme, že vlivem ohřátí se společná plocha roztáhne v osovém směru o 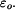
Ve vzdálenosti z od této plochy bude osové prodloužení rovno (obr. 2)
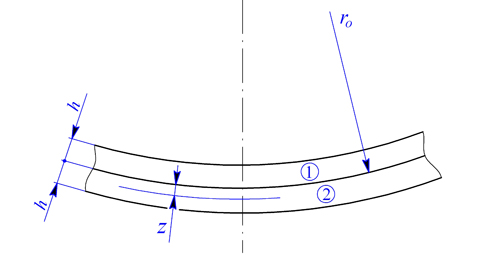
Obr. 2
Osové prodloužení v jednotlivých částech nosníku bude
dosadíme-li do levé strany těchto rovnic za 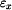 máme pro napětí vztahy
máme pro napětí vztahy
Z podmínky rovnováhy sil v průřezu vyjde:
Z podmínky rovnováhy momentů vyjde
Do rovnic dosadíme vztahy pro napětí.
Z těchto rovnic vyjádříme prodloužení 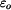 a zakřivení
a zakřivení  společné plochy a po dosazení do vztahů pro napětí získáme napětí v každé části bimetalu.
společné plochy a po dosazení do vztahů pro napětí získáme napětí v každé části bimetalu.
Průhyb bimetalu závisí slabě na poměru 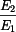 , avšak je silně ovlivněn rozdílem teplotních roztažností
, avšak je silně ovlivněn rozdílem teplotních roztažností 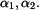 . Položíme-li přibližně
. Položíme-li přibližně 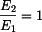 , pak dostáváme
, pak dostáváme
a napětí budou
zpracoval:Miroslav Denk
Užití Castiglianovy věty pro výpočet teplotních napětí
Příklad 1.
Prutová soustava tvořená třemi pruty (obr. 1) je ze stejného materiálu (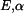 ) a stejného průřezu
) a stejného průřezu 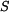 . Určete jaká napětí vzniknou v prutech po zahřátí prutové soustavy o teplotu
. Určete jaká napětí vzniknou v prutech po zahřátí prutové soustavy o teplotu 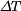 . Soustava je opět symetrická. Výpočet pomocí deformační podmínky je uveden v kapitole Teplotní napětí v tyčích namáhaných na tah nebo tlak. , příklad 7.
. Soustava je opět symetrická. Výpočet pomocí deformační podmínky je uveden v kapitole Teplotní napětí v tyčích namáhaných na tah nebo tlak. , příklad 7.

Obr. 1
Doplňková deformační energie soustavy
Podmínka rovnováhy je 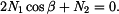
Zvolme 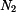 za staticky neurčitou sílu, pak platí
za staticky neurčitou sílu, pak platí 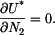
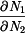 určíme z podmínky rovnováhy
určíme z podmínky rovnováhy 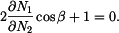
Po dosazení dostaneme rovnici
ze které a z podmínky rovnováhy určíme
zpracoval:Miroslav Denk
Příklad 2.
Jaká napětí vzniknou v prutech soustavy (obr. 1), ohřeje-li se pouze prut 1. Soustava prutů již není symetrická a sestavení deformační podmínky by bylo pracné. Doplňková deformační energie soustavy je

Obr. 1
kde stále platí rovnice rovnováhy a tedy 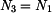 . Zvolme
. Zvolme 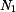 za staticky neurčitou veličinu, pak platí:
za staticky neurčitou veličinu, pak platí:
Odtud
zpracoval:Miroslav Denk
Příklad 3.
Nosník na třech podporách podle obr. 1 je ohřát o přírůstek teploty. 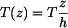 (viz. příkladu 6.)
(viz. příkladu 6.)
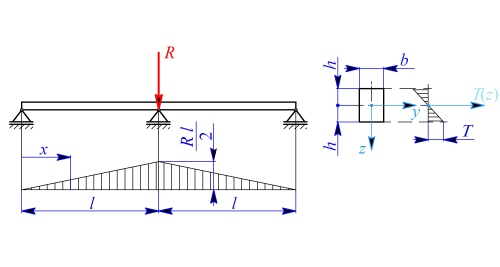
Obr. 1
Řešení: Ve střední podpoře vznikne reakce, která vyvolá ohybový moment
Napětí v nosníku
Doplňková deformační energie
Platí
kde
Odtud
zpracoval:Miroslav Denk
Příklad 4.
Příklad 5.
Tenká obruč je bez napětí vložena mezi dvě tuhé opory v bodech A a B podle obr. 1. Určete reakce v podporách po ohřátí celé obruče o teplotu  . Dáno:
. Dáno: 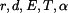 . Řešení je možné jen pomocí energetické metody. Příklad je 2-krát staticky neurčitý.
. Řešení je možné jen pomocí energetické metody. Příklad je 2-krát staticky neurčitý.
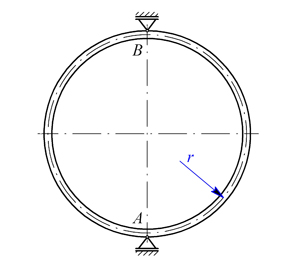
Obr. 1
Řešení:
1) V tomto případě použijeme vztah pro energii napjatosti U a deformační podmínku. Uvolníme-li obruč a zahřejeme-li jí o teplotu  , změní se vzdálenosti
, změní se vzdálenosti 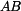 o přírůstek
o přírůstek 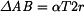 . V podporách tedy musí vzniknout síly
. V podporách tedy musí vzniknout síly  , které by průměr obruče stlačily o tuto vzdálenost.
, které by průměr obruče stlačily o tuto vzdálenost.
Deformační podmínka je
kde 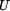 je deformační energie.
je deformační energie.
Z podmínky rovnováhy podle obr. 2 vyjde 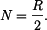
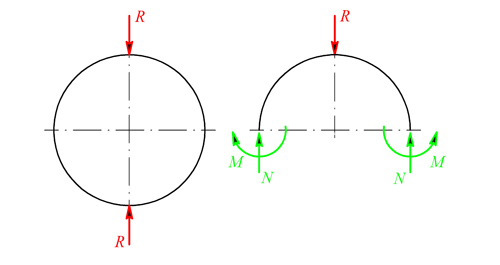
Obr. 2
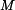 je staticky neurčitý vnitřní moment, proto platí
je staticky neurčitý vnitřní moment, proto platí
Energie napjatosti je
kde
2) Řešení pomocí doplňkové deformační energie 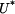 . V tomto případě použijeme 2-krát větu o minimu deformační práce a bude platit
. V tomto případě použijeme 2-krát větu o minimu deformační práce a bude platit
Doplňkovou energii vypočteme z hustoty deformační energie
kde
Do normálného napětí musíme zahrnout i vliv normálné síly 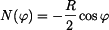 v průřezu obruče (obr. 3).
v průřezu obruče (obr. 3).

Obr. 3
Parciální derivace jsou 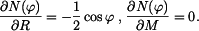
Dostaneme soustavu dvou rovnic
Z první rovnice opět vyjde 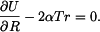
zpracoval:Miroslav Denk
Kruhové desky namáhané na ohyb
Příklad 1.
Volná tenká mezikruhová deska podle obr. 1 je zatížena přírůstkem teploty, který je lineární funkcí vzdálenosti od střední roviny 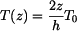 . Určete napětí a deformaci desky.
Dáno:
. Určete napětí a deformaci desky.
Dáno: 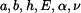 a přírůstek teploty je
a přírůstek teploty je 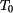 .
.
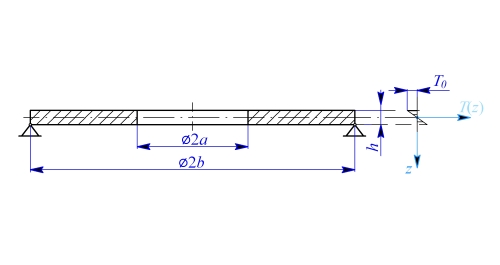
Obr. 1
Řešení:
Příčná síla v desce nevzniká: 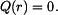
Teplotní moment 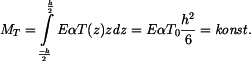
Radiální a tečný moment v desce jsou
Radiální moment na okrajích desky je roven nule, tedy 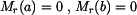 . Odtud vypočteme konstanty
. Odtud vypočteme konstanty
Křivosti desky po deformaci jsou
Průhyb
kde z okrajové podmínky 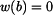 vypočteme
vypočteme
Průhyb desky na poloměru  pak bude
pak bude 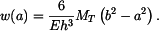
Deska je bez napětí, pouze se prohne. Natočení desky na poloměru  bude:
bude:
zpracoval:Miroslav Denk
Příklad 2.
Deska z příkladu 1. je vetknutá na vnějším i vnitřním okraji (obr. 1). Jaká vzniknou v desce napětí? Průběh teploty je opět 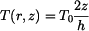
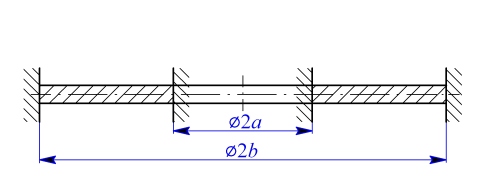
Obr. 1
Řešení: Vzhledem k tomu, že 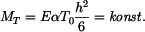 nezávisí na poloměru, deska se neprohne. Tečné a radiální momenty budou stejné a konstantní
nezávisí na poloměru, deska se neprohne. Tečné a radiální momenty budou stejné a konstantní
zpracoval:Miroslav Denk
Příklad 3.
Deska z příkladu 1. je vetknutá na vnitřním okraji a na vnějším okraji je volná (obr. 1). Jaká vzniknou v desce napětí?
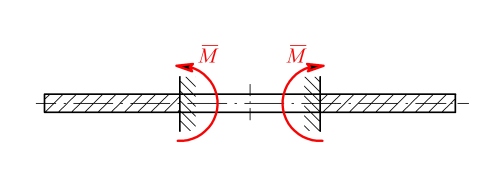
Obr. 1
Řešení: Na desku bude působit z vetknutí na vnitřním okraji radiální moment 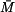 . Musí být tak velký, aby sám o sobě způsobil na poloměru a stejné natočení, jako vzniká v důsledku teplotního zatížení u volné desky - tedy (podle příkladu 1.)
. Musí být tak velký, aby sám o sobě způsobil na poloměru a stejné natočení, jako vzniká v důsledku teplotního zatížení u volné desky - tedy (podle příkladu 1.)
Pro 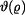 a
a 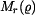 při zatížení momentem
při zatížení momentem 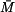 platí
platí
kde 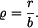
Okrajové podmínky jsou
Po dosazení do okrajových podmínek dostaneme konstanty 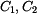
Sklon tečné roviny je
a na vnitřním okraji platí
Ze srovnání obou natočení v místě vetknutí
získáme velikost 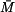
Radiální a tečný moment jsou
zpracoval:Miroslav Denk
Příklad 4.
Deska z příkladu 1. je prostě podepřená na obou okrajích (obr. 1). Jaké vznikne napětí v desce?
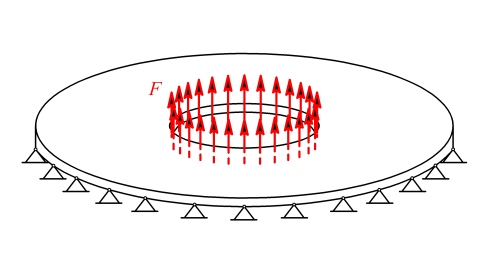
Obr. 1
Řešení: Kdyby byla deska podepřená pouze na vnějším okraji, pak po teplotním zatížení bude bez napětí a průhyb na jejím vnitřním okraji bude podle příkladu 1.
Je-li deska podepřena na obou okrajích, musí vnitřní podpora působit na desku celkovou silou 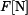 , která by sama prohnula desku na vnitřním okraji o
, která by sama prohnula desku na vnitřním okraji o 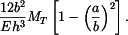
Příčná síla v desce 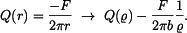
Pravá strana diferenciální rovnice je 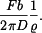
Vztah pro sklon tečné roviny 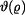 je
je
Konstanty určíme z okrajových podmínek
Po dosazení
Průhyb desky
Konstantu 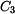 určíme z podmínky
určíme z podmínky 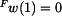 - průhyb na vnějším okraji je roven
- průhyb na vnějším okraji je roven 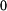 a odtud
a odtud
Po dosazení 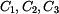 do vztahu pro průhyb
do vztahu pro průhyb 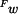 můžeme vypočítat průhyb
můžeme vypočítat průhyb 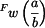 na vnitřním okraji. Z podmínky
na vnitřním okraji. Z podmínky 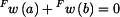 dostaneme sílu
dostaneme sílu 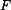 (reakci v podpoře). Po dosazení
(reakci v podpoře). Po dosazení 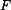 do vztahů pro momenty dostaneme napětí v desce.
do vztahů pro momenty dostaneme napětí v desce.
zpracoval:Miroslav Denk
Kotouče a dlouhé válce
Příklad 1.
Tenký ocelový kotouč podle obr. 1 je při počáteční teplotě 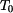 bez napětí. Vnějšímu okraji kotouče je zabráněno v roztažení. Jaké napětí vznikne v kotouči, ohřeje-li se celý zvolna o teplotu
bez napětí. Vnějšímu okraji kotouče je zabráněno v roztažení. Jaké napětí vznikne v kotouči, ohřeje-li se celý zvolna o teplotu  ?
?
Dáno: 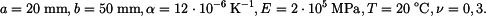

Obr. 1
Řešení:Kdyby byl kotouč volný, pak při ohřátí o teplotu 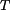 by se každý jeho poloměr zvětšil o
by se každý jeho poloměr zvětšil o  , tedy poloměr
, tedy poloměr 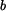 by se zvětšil o
by se zvětšil o 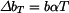 . Tomuto rozšíření brání okolí kotouče, mezi kotoučem a okolím vznikne tlak
. Tomuto rozšíření brání okolí kotouče, mezi kotoučem a okolím vznikne tlak  . Jeho velikost určíme z deformační podmínky
. Jeho velikost určíme z deformační podmínky 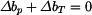 .
.
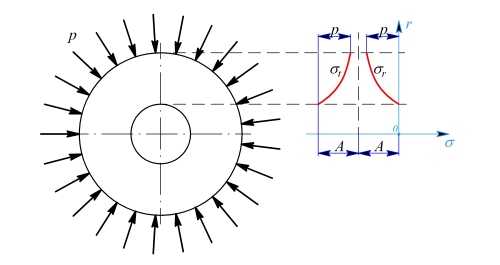
Obr. 2
Konstanta

je
Napětí na vnějším okraji kotouče jsou (obr. 2)
Odpovídající deformace je
Z deformační podmínky
vypočteme 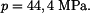
Nejméně příznivá napjatost je jednoosá napjatost na poloměru  . Napětí je rovno
. Napětí je rovno 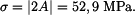
zpracoval:Miroslav Denk
Příklad 2.
Tenký kotouč podle obr. 1 byl při teplotě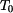 bez napětí. Jeho čelní plochy jsou teplotně izolovány, ale nic nebrání v jejich volné dilataci. Tento kotouč byl zvolna zahřát tak, že vznikne ustálený tepelný stav, kdy na vnitřním okraji kotouče je teplota
bez napětí. Jeho čelní plochy jsou teplotně izolovány, ale nic nebrání v jejich volné dilataci. Tento kotouč byl zvolna zahřát tak, že vznikne ustálený tepelný stav, kdy na vnitřním okraji kotouče je teplota 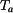 a na vnějším okraji kotouče je teplota
a na vnějším okraji kotouče je teplota 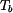 . Jaké je napětí v kotouči?
. Jaké je napětí v kotouči?
Dáno: 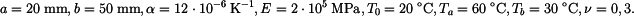
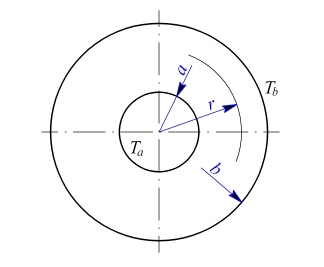
Obr. 1
Řešení: V kotouči vzniká ustálené teplotní pole, které je osově symetrické, teplota se po tloušťce kotouče nemění. Jedná se o rovinnou napjatost - nevznikne osové napětí. Rovnice vedení tepla má v tomto případě tvar
Za vztažný poloměr zvolíme vnější poloměr kotouče 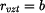 . Řešení této rovnice je funkcí teploty
. Řešení této rovnice je funkcí teploty
kde integrační konstanty 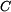 a
a 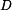 určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
Odtud
Diferenciální rovnice pro radiální posuv v případě rovinné napjatosti:
Z homogenního řešení 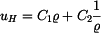 dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
kde integrační konstanty  a
a  určujeme z podmínek na okraji kotouče.
určujeme z podmínek na okraji kotouče.
Diferenciální rovnici pro radiální posuv vynásobíme  a dosadíme za funkci
a dosadíme za funkci 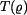 . Na pravé straně dostáváme:
. Na pravé straně dostáváme: 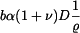 . Označme
. Označme  . Partikulární řešení bude v tomto případě
. Partikulární řešení bude v tomto případě
a napětí z tohoto řešení odvozená jsou
Sečtěme homogenní řešení a partikulární řešení a přidáme teplotní člen 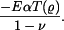 Dostaneme napětí
Dostaneme napětí
Integrační konstanty  a
a  určíme z podmínek pro volné okraje:
určíme z podmínek pro volné okraje:
Po dosazení
Rovnice můžeme dále upravovat a konstanty A a B vyjádřit obecně pro tento typ zatížení a okrajových podmínek. Rozumnější bude v této fázi konstanty, které mají rozměr napětí, vypočítat numericky. Vyjde 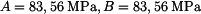 . Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.
. Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.
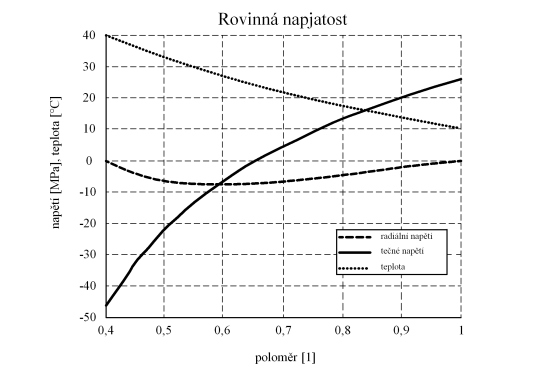
Obr. 2
Kdybychom zabránili volné změně tloušťky kotouče, vzniklo by v kotouči osové napětí 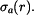 Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak
Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak 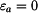 a jedná se o tzv. rovinnou deformaci. Určíme napětí
a jedná se o tzv. rovinnou deformaci. Určíme napětí 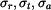 v tomto případě. Pro poměrné deformace máme nyní vztahy
v tomto případě. Pro poměrné deformace máme nyní vztahy
Z poslední rovnice získáme 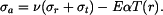
Na pravé straně diferenciální rovnice pro radiální posuv  je v případu rovinné deformace výraz
je v případu rovinné deformace výraz
Zde obdobně zavedeme 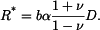
Z homogenního řešení rovnice 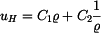 máme opět
máme opět
(konstanty 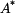 a
a 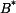 mají jinou hodnotu, než
mají jinou hodnotu, než  a
a  v předchozím řešení).
v předchozím řešení).
Partikulární řešení
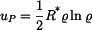 dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
K součtu jednotlivých částí napětí musíme ještě připojit teplotní člen 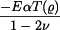 :
:
Axiální napětí bude
Z podmínek na okrajích kotouče 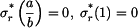 určíme konstanty
určíme konstanty 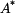 a
a 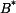 , které dosadíme do vztahů pro napětí, pak
, které dosadíme do vztahů pro napětí, pak
Průběh napětí je na obr. 3.
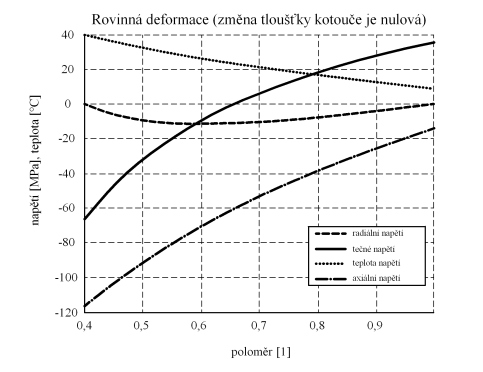
Obr. 3
Pozn.: Vztahy pro napětí 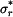 a
a 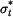 v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy
v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy 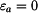 ) můžeme dostat přímo ze vztahů
) můžeme dostat přímo ze vztahů 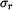 a
a 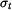 pro rovinnou napjatost (volná dilatace tloušťky
pro rovinnou napjatost (volná dilatace tloušťky 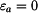 ), jestliže do nich dosadíme za Youngův modul
), jestliže do nich dosadíme za Youngův modul 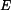 vztah
vztah 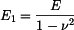 , za teplotní roztažnost
, za teplotní roztažnost  vztah
vztah 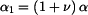 a za Poissonovu konstantu
a za Poissonovu konstantu  vztah
vztah 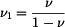 . (Je třeba dosadit i do výrazu pro konstantu
. (Je třeba dosadit i do výrazu pro konstantu  .)
.)
zpracoval:Miroslav Denk
Příklad 3.
Mějme dlouhý dutý válec s rozměry 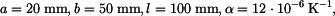
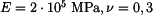 , s počáteční teplotou
, s počáteční teplotou 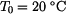 s ustáleným teplotním polem
s ustáleným teplotním polem 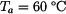 ,
, 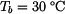 (stejné parametry jako v příkladu 2.). Nic nebrání v jeho délkové dilataci.
(stejné parametry jako v příkladu 2.). Nic nebrání v jeho délkové dilataci. 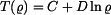 . Jaká vzniknou ve válci napětí?
. Jaká vzniknou ve válci napětí?
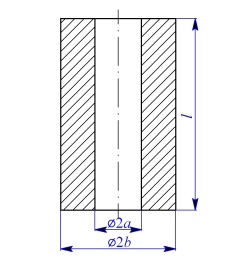
Obr. 1
Řešení: Jedná se o rovinnou deformaci, kdy v dostatečné vzdálenosti od konců je 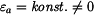 . Použijeme vztahy pro deformace při trojosé napjatosti a vypočteme axiální napětí
. Použijeme vztahy pro deformace při trojosé napjatosti a vypočteme axiální napětí
Ve vztazích pro napětí 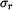 a
a 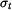 tedy přibude konstantní člen
tedy přibude konstantní člen 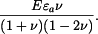
Pravá strana diferenciální rovnice pro radiální posuv se nezmění, tedy
Vztahy pro napětí jsou
a axiální napětí je
Konstanty 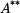 a
a 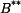 určíme z okrajových podmínek
určíme z okrajových podmínek
Odtud
tedy 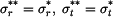 (napětí budou stejná jako v předchozím příkladě)
(napětí budou stejná jako v předchozím příkladě)
a konstantu 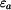 určíme z podmínky
určíme z podmínky
Prodloužení válce bude 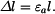
zpracoval:Miroslav Denk
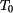 , při které byla bez napětí, o teplotu
, při které byla bez napětí, o teplotu 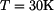 . Jaké napětí vznikne v kolejnici, je-li
. Jaké napětí vznikne v kolejnici, je-li 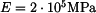 ,
, 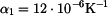 ?
?

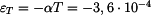 .
.
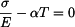
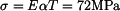
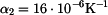 je oboustranně vetknutá. Vypočtěte napětí v jejích jednotlivých částech, je-li
je oboustranně vetknutá. Vypočtěte napětí v jejích jednotlivých částech, je-li 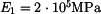 ,
, 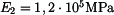 ,
, 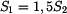 ,
,  , ohřeje-li se celá o
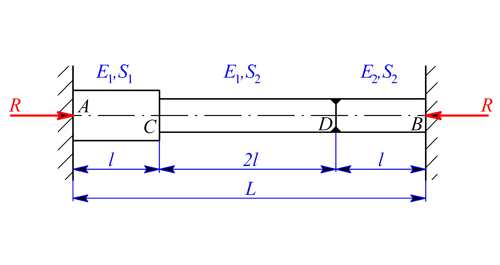
, ohřeje-li se celá o 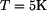 .
.
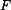 je:
je: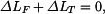
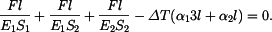
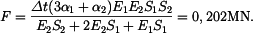
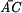 je:
je: 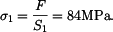
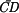 a
a 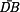 je:
je: 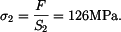
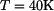 . Vypočtěte napětí v tyči. Dáno:
. Vypočtěte napětí v tyči. Dáno: 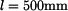 ,
, 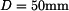 ,
, 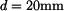 ,
, 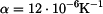 .
.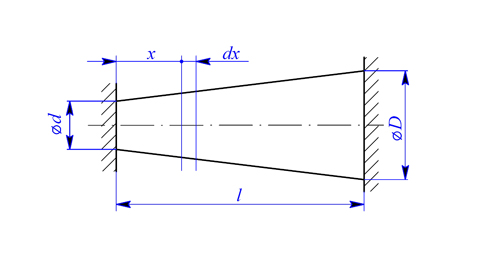
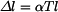 . V tyči vznikne tlakové napětí, které eliminuje toto prodloužení. Předpokládejme, že ve vetknutí vznikne reakce
. V tyči vznikne tlakové napětí, které eliminuje toto prodloužení. Předpokládejme, že ve vetknutí vznikne reakce  od levého vetknutí bude napětí
od levého vetknutí bude napětí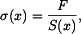
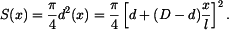
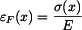 a zkrácení elementu
a zkrácení elementu 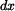 bude
bude 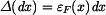 . Zkrácení tyče vlivem napětí musí být stejné, jako její prodloužení vlivem teploty.
. Zkrácení tyče vlivem napětí musí být stejné, jako její prodloužení vlivem teploty.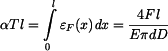
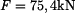 a maximální napětí na levém konci tyče
a maximální napětí na levém konci tyče 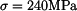 .
.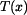 bude nyní funkcí souřadnice
bude nyní funkcí souřadnice 
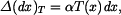
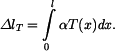
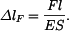
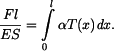
 ?
?
 ,
, 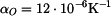 ). Prodloužení obou částí však musí být stejné. V trubce vznikne tlakové a v tyči tahové napětí. Deformační podmínka je
). Prodloužení obou částí však musí být stejné. V trubce vznikne tlakové a v tyči tahové napětí. Deformační podmínka je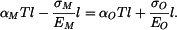

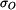 a
a 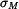 .
.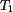 ,
, 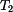 ). Jaké napětí vznikne v tyčích, jestliže tuhé čelo se nemůže natočit?
). Jaké napětí vznikne v tyčích, jestliže tuhé čelo se nemůže natočit? 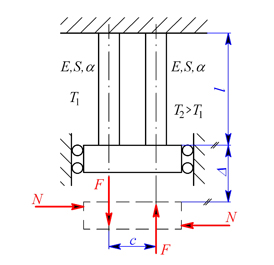
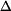 , která je rovna prodloužení tyčí. Na tyče působí osové síly
, která je rovna prodloužení tyčí. Na tyče působí osové síly 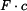 je v rovnováze s momentem sil
je v rovnováze s momentem sil 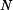 , které vznikají ve vedení. Z podmínky stejné délky tyčí po ohřátí
, které vznikají ve vedení. Z podmínky stejné délky tyčí po ohřátí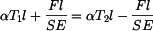
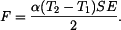

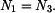
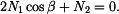
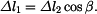
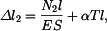
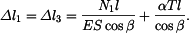
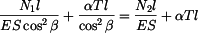
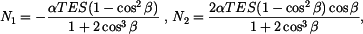
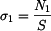 ,
, 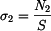
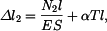
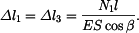
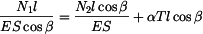
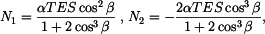
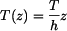 . Dáno:
. Dáno: 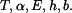 Určete napětí v tyči a deformaci tyče.
Určete napětí v tyči a deformaci tyče.

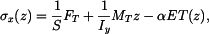
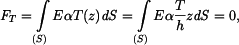
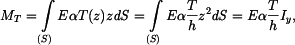
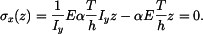
 ).
).
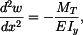
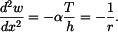
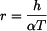 . Tyč se neprodlouží, neboť střední posuv průřezu je nulový:
. Tyč se neprodlouží, neboť střední posuv průřezu je nulový:
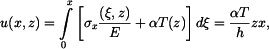
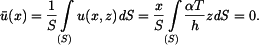

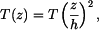
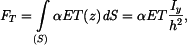

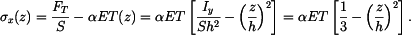
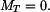

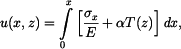
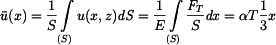
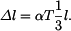

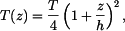
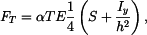
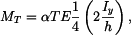
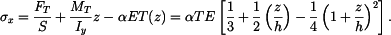
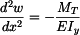
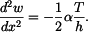
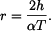
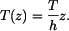

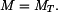 Napětí, které vznikne v tyči má lineární průběh
Napětí, které vznikne v tyči má lineární průběh
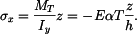

 , která bude bránit průhybu nosníku směrem vzhůru. Moment v obecném řezu je
, která bude bránit průhybu nosníku směrem vzhůru. Moment v obecném řezu je
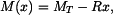
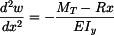

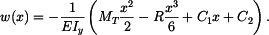
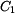 a
a 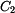 určíme z okrajových podmínek pro deformaci nosníku
určíme z okrajových podmínek pro deformaci nosníku
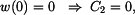

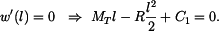
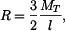
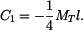

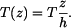 Určete napětí a deformaci nosníku.
Určete napětí a deformaci nosníku.

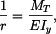
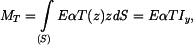
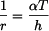
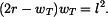
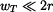 , lze napsat
, lze napsat
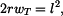
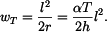

 uprostřed je průhyb (obr. 3)
uprostřed je průhyb (obr. 3)


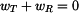 vyjde
vyjde
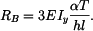
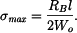
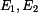 a součinitele teplotní roztažnosti
a součinitele teplotní roztažnosti 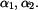

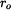 , dále předpokládejme, že vlivem ohřátí se společná plocha roztáhne v osovém směru o
, dále předpokládejme, že vlivem ohřátí se společná plocha roztáhne v osovém směru o 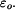
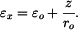

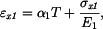
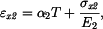
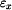 máme pro napětí vztahy
máme pro napětí vztahy
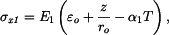
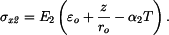
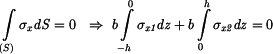
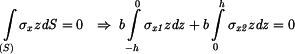
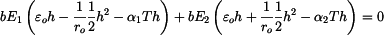
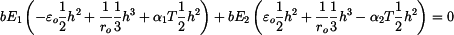
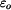 a zakřivení
a zakřivení  společné plochy a po dosazení do vztahů pro napětí získáme napětí v každé části bimetalu.
společné plochy a po dosazení do vztahů pro napětí získáme napětí v každé části bimetalu.
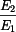 , avšak je silně ovlivněn rozdílem teplotních roztažností
, avšak je silně ovlivněn rozdílem teplotních roztažností 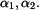 . Položíme-li přibližně
. Položíme-li přibližně 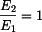 , pak dostáváme
, pak dostáváme
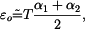
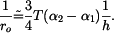
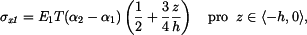
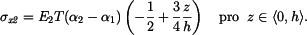
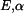 ) a stejného průřezu
) a stejného průřezu 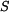 . Určete jaká napětí vzniknou v prutech po zahřátí prutové soustavy o teplotu
. Určete jaká napětí vzniknou v prutech po zahřátí prutové soustavy o teplotu 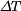 . Soustava je opět symetrická. Výpočet pomocí deformační podmínky je uveden v kapitole
. Soustava je opět symetrická. Výpočet pomocí deformační podmínky je uveden v kapitole 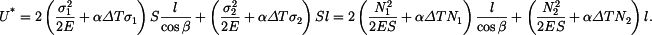
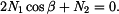
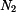 za staticky neurčitou sílu, pak platí
za staticky neurčitou sílu, pak platí 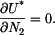
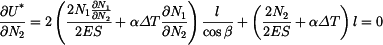
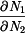 určíme z podmínky rovnováhy
určíme z podmínky rovnováhy 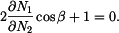
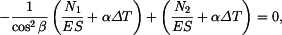
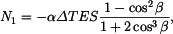
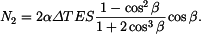
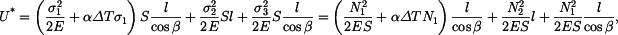
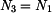 . Zvolme
. Zvolme 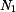 za staticky neurčitou veličinu, pak platí:
za staticky neurčitou veličinu, pak platí:
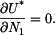
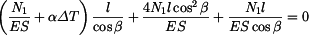
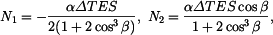
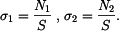
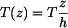 (viz.
(viz. 
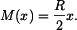
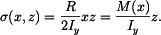
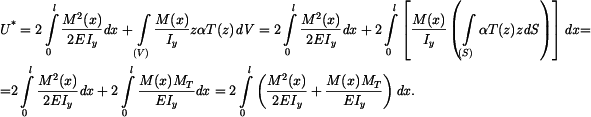
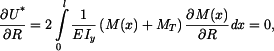
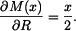
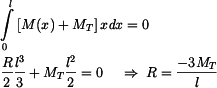
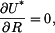
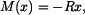
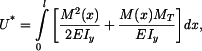
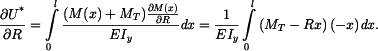
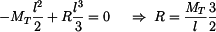
 . Řešení je možné jen pomocí energetické metody. Příklad je 2-krát staticky neurčitý.
. Řešení je možné jen pomocí energetické metody. Příklad je 2-krát staticky neurčitý.

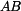 o přírůstek
o přírůstek 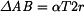 . V podporách tedy musí vzniknout síly
. V podporách tedy musí vzniknout síly 
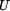 je deformační energie.
je deformační energie.
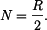

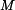 je staticky neurčitý vnitřní moment, proto platí
je staticky neurčitý vnitřní moment, proto platí
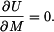
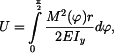
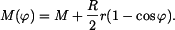
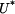 . V tomto případě použijeme 2-krát větu o minimu deformační práce a bude platit
. V tomto případě použijeme 2-krát větu o minimu deformační práce a bude platit
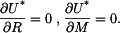
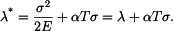
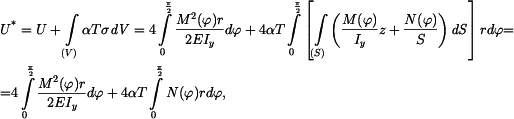
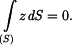
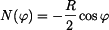 v průřezu obruče (obr. 3).
v průřezu obruče (obr. 3).

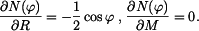
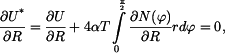
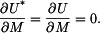
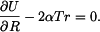
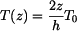 . Určete napětí a deformaci desky.
Dáno:
. Určete napětí a deformaci desky.
Dáno: 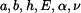 a přírůstek teploty je
a přírůstek teploty je 
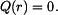
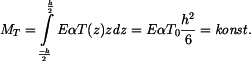
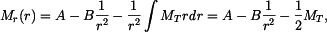
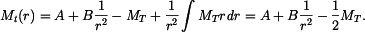
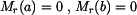 . Odtud vypočteme konstanty
. Odtud vypočteme konstanty
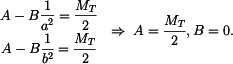
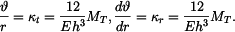
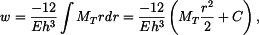
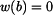 vypočteme
vypočteme
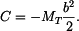
 pak bude
pak bude 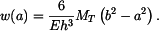
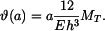
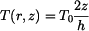

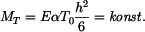 nezávisí na poloměru, deska se neprohne. Tečné a radiální momenty budou stejné a konstantní
nezávisí na poloměru, deska se neprohne. Tečné a radiální momenty budou stejné a konstantní
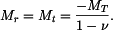

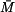 . Musí být tak velký, aby sám o sobě způsobil na poloměru a stejné natočení, jako vzniká v důsledku teplotního zatížení u volné desky - tedy (podle
. Musí být tak velký, aby sám o sobě způsobil na poloměru a stejné natočení, jako vzniká v důsledku teplotního zatížení u volné desky - tedy (podle 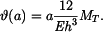
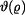 a
a 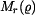 při zatížení momentem
při zatížení momentem 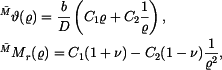
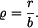
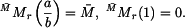
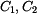
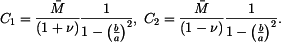
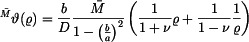
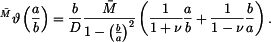
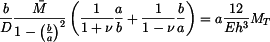
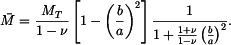
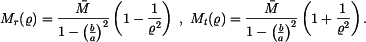

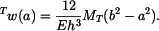
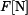 , která by sama prohnula desku na vnitřním okraji o
, která by sama prohnula desku na vnitřním okraji o 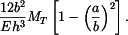
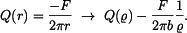
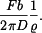
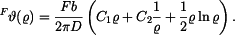
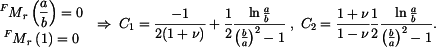
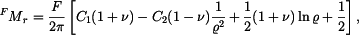
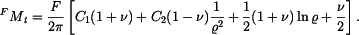
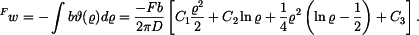
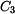 určíme z podmínky
určíme z podmínky 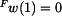 - průhyb na vnějším okraji je roven
- průhyb na vnějším okraji je roven  a odtud
a odtud
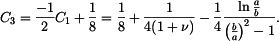
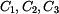 do vztahu pro průhyb
do vztahu pro průhyb 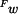 můžeme vypočítat průhyb
můžeme vypočítat průhyb 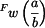 na vnitřním okraji. Z podmínky
na vnitřním okraji. Z podmínky 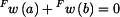 dostaneme sílu
dostaneme sílu 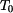 bez napětí. Vnějšímu okraji kotouče je zabráněno v roztažení. Jaké napětí vznikne v kotouči, ohřeje-li se celý zvolna o teplotu
bez napětí. Vnějšímu okraji kotouče je zabráněno v roztažení. Jaké napětí vznikne v kotouči, ohřeje-li se celý zvolna o teplotu 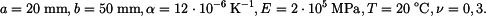

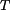 by se každý jeho poloměr zvětšil o
by se každý jeho poloměr zvětšil o  , tedy poloměr
, tedy poloměr 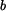 by se zvětšil o
by se zvětšil o 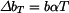 . Tomuto rozšíření brání okolí kotouče, mezi kotoučem a okolím vznikne tlak
. Tomuto rozšíření brání okolí kotouče, mezi kotoučem a okolím vznikne tlak  . Jeho velikost určíme z deformační podmínky
. Jeho velikost určíme z deformační podmínky 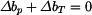 .
.

 je
je
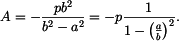
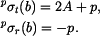

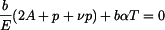
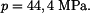
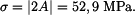
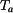 a na vnějším okraji kotouče je teplota
a na vnějším okraji kotouče je teplota 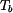 . Jaké je napětí v kotouči?
. Jaké je napětí v kotouči?
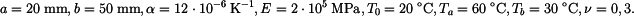

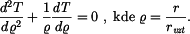
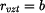 . Řešení této rovnice je funkcí teploty
. Řešení této rovnice je funkcí teploty
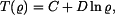
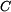 a
a 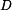 určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
určíme z okrajových podmínek pro vnitřní a vnější poloměr, tedy
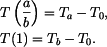
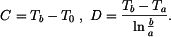
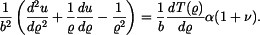
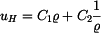 dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
dostáváme známé vztahy pro napětí v rotačně symetrických tenkých kotoučích
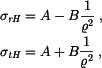
 určujeme z podmínek na okraji kotouče.
určujeme z podmínek na okraji kotouče.
 a dosadíme za funkci
a dosadíme za funkci 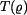 . Na pravé straně dostáváme:
. Na pravé straně dostáváme: 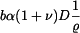 . Označme
. Označme  . Partikulární řešení bude v tomto případě
. Partikulární řešení bude v tomto případě
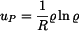
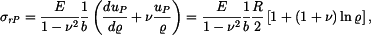
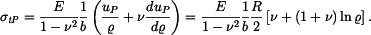
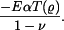 Dostaneme napětí
Dostaneme napětí
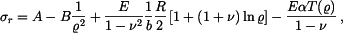
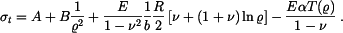
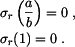
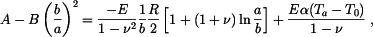

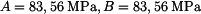 . Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.
. Průběh radiálního a tečného napětí je na obr. 2. V tomto případě rovinné napjatosti nastane deformace v axiálním směru. Tloušťka kotouče se bude zvětšovat všude a nerovnoměrně v závislosti na poloměru.

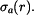 Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak
Předpokládejme, že změně tloušťky je zcela zabráněno vnější vazbou, pak 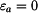 a jedná se o tzv. rovinnou deformaci. Určíme napětí
a jedná se o tzv. rovinnou deformaci. Určíme napětí 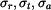 v tomto případě. Pro poměrné deformace máme nyní vztahy
v tomto případě. Pro poměrné deformace máme nyní vztahy
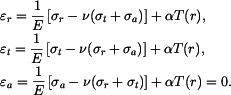
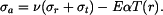
 je v případu rovinné deformace výraz
je v případu rovinné deformace výraz
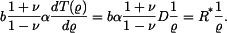
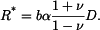
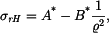
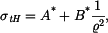
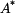 a
a 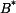 mají jinou hodnotu, než
mají jinou hodnotu, než 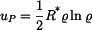 dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
dosadíme do vztahů pro radiální a tečné napětí (tyto vztahy platí pro rovinnou deformaci a jsou různé od vztahů pro napětí v předchozí části příkladu, kdy se jednalo o rovinnou napjatost):
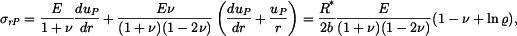
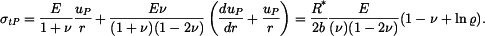
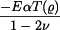 :
:
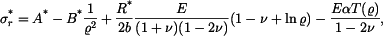
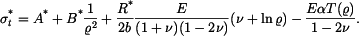
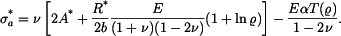
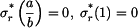 určíme konstanty
určíme konstanty 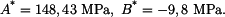

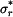 a
a 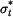 v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy
v případu rovinné deformace (kotouči je bráněno v dilataci tloušťky, tedy 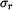 a
a 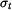 pro rovinnou napjatost (volná dilatace tloušťky
pro rovinnou napjatost (volná dilatace tloušťky 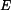 vztah
vztah 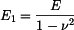 , za teplotní roztažnost
, za teplotní roztažnost  vztah
vztah 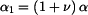 a za Poissonovu konstantu
a za Poissonovu konstantu  vztah
vztah 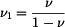 . (Je třeba dosadit i do výrazu pro konstantu
. (Je třeba dosadit i do výrazu pro konstantu 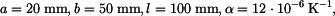
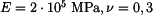 , s počáteční teplotou
, s počáteční teplotou 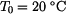 s ustáleným teplotním polem
s ustáleným teplotním polem 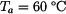 ,
, 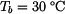 (stejné parametry jako v
(stejné parametry jako v 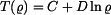 . Jaká vzniknou ve válci napětí?
. Jaká vzniknou ve válci napětí?

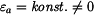 . Použijeme vztahy pro deformace při trojosé napjatosti a vypočteme axiální napětí
. Použijeme vztahy pro deformace při trojosé napjatosti a vypočteme axiální napětí
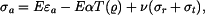
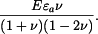
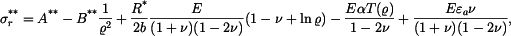
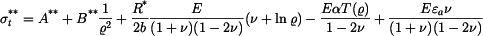
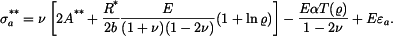
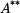 a
a 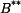 určíme z okrajových podmínek
určíme z okrajových podmínek
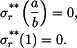
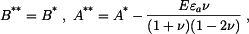
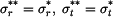 (napětí budou stejná jako v předchozím
(napětí budou stejná jako v předchozím 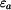 určíme z podmínky
určíme z podmínky